Praktische Einführung
Ein Beitrag von Sebastian Schmidt
Menschenkundlicher Hintergrund
Die Zahl Eins steht qualitativ gesehen für die Einheit. Es gibt riesige Einheiten wie z.B. unsere Erde oder kleinere Einheiten wie eine Tomate oder individuelle Einheiten wie meine Familie. Allen gemeinsam ist, dass sie immer eine Ganzheit ins Auge fassen. Diese Ganzheit wird zunächst nicht differenziert oder unterteilt. Bei der Bruchrechnung teilen wir jedoch Einheiten. Der Name selbst drückt es etwas drastischer aus: Es geht etwas zu Bruch.
In den Kindern geschieht im Übergang von der 3. zur 4. Klasse seelisch-geistig gesehen etwas Ähnliches. Sie überschreiten den so genannten Rubikon. Auch hier geht etwas zu Bruch: Die gefühlte Einheit von Kind und Welt oder präziser von Kind und Eltern, von Kind und Lehrer usw. zeigt für das Erleben des Kindes die ersten großen Risse. Es spürt und erlebt sich selbst und die ihn umgebenden Menschen und Dinge mehr und mehr in ihrem Eigensein. So unbeschwert die Zeit bis dahin auch gewesen sein mag, das Kind muss diesen kleineren oder auch größeren Schmerz erleben, um sich vom Umkreis zu lösen und seine eigenständige Persönlichkeit zu bilden – eine entwicklungsbedingte Notwendigkeit.
So gesehen findet in der Bruchrechnung und im Leben des Kindes um das 9./10. Lebensjahr ein ähnlicher Prozess statt: Die gefühlte Einheit von Ich und Welt zerbricht – neue Bezüge zwischen Menschen und Dingen müssen gefunden werden. Daher ist das innere Verständnis bezüglich der Bruchrechnung im 4. Schuljahr auch besonders groß.
Praktisch
Die erste Epoche zur Bruchrechnung begann damit, dass jedes Kind einen leicht zu durchbrechenden Stock mitbringen sollte, der etwas die Länge seiner Körpergröße hatte. Wir verteilten uns im Klassenraum mit genügend Platz um uns herum. Alle Kinder maßen mit dem Auge die Hälfte des Stockes, stellten sich auf ein Bein und brachen mit dem angewinkelten Knie den Stock in der Mitte durch. Das weckte Emotionen. Bei manchen brach der Stock nicht, andere waren stolz auf ihr Werk und wollten es zeigen. Nach einem kurzen gemeinsamen Austausch darüber öffneten wir unsere Epochenhefte und zeichneten auf die erste Seite unseren ganzen Stock und schrieben darüber „ein Stock“. Dann zeichneten wir die beiden Hälften darunter und schrieben dazu:
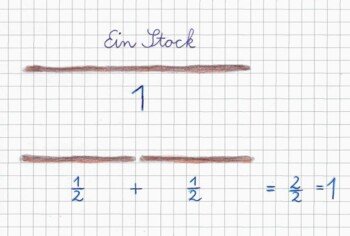
Der Bruchstrich wurde erläutert. Er ist im Grunde ein quergelegtes Geteiltzeichen. Zu ½ kann man also sagen: „Ich habe einen Stock und teile ihn in zwei Hälften.“ Dann kamen einfache „Kommandos“, welche den Kindern in diesem Lebensalter noch viel Freude bereiten und das Bewusstsein zweier Teile stärken: „Haltet eine Hälfe vom Stock in die Höhe, jetzt die andere. Haltet nun zwei Hälften in die Höhe, führt sie zusammen und macht den Stock wieder ganz. Legt eine Hälfte unter den Tisch, die andere auf den Tisch … Legt beide Hälften nebeneinander auf den Tisch.“
Nun nahmen wir eine Hälfte, suchten uns wiederum einen freien Platz im Klassenraum und brachen erneut die Hälfte in zwei Viertel. Die beiden Viertel legten wir jetzt wieder auf den Tisch neben die Hälfte. „Was fällt euch auf, wenn Ihr die Stöcke anseht?“ Ich halte diese Momente des Innehaltens für wichtig, damit insbesondere die Kinder, die kopflos in der Aktion aufgehen, kurz zentriert werden. Folgende Antworten kamen: „Zwei sind kürzer, einer ist lang.“ „Die kürzeren sind halb so lang, wie der lange Stock.“ „Meiner ist nicht genau in der Hälfte gebrochen.“ … Jetzt brachen wir gemeinsam die zweite Hälfte und legten anschließend alle Viertel nebeneinander auf unseren Tisch. Im Heft notierten wir:
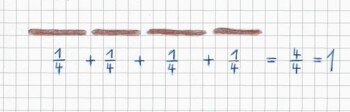
Beim Aufschreiben der Brüche sprachen wir zusammen: „Eins geteilt durch vier ist ein Viertel.“ Dann folgten wieder verschiedene „Kommandos“: „Haltet ein Viertel in die Höhe. Haltet zwei Viertel in die Höhe. Haltet drei Viertel in die Höhe. Haltet vier Viertel in die Höhe. Haltet die Hälfte aller Viertel in die Höhe. Legt auf den Boden alle wieder aneinander. Welche Form lässt sich aus den vier Vierteln ganz einfach legen?“ Natürlich ein Quadrat. Alle taten es.
Bei diesen Eindrücken beließ ich es für den heutigen Tag. Eine Hausaufgabe für morgen bestand darin, eine Banane, ein Messer und ein Frühstücksbrettchen mitzubringen.
2. Tag
Gleich am Anfang des Unterrichts packten alle Kinder ihre Bananen, Messer und Brettchen aus. Wieder hatten wir eine Einheit. Dieses Mal wollte ich mit den Kindern dritteln. Nach dem Schälen der Banane wurde mit dem Auge Maß genommen und erst nur leicht eingeritzt. Gab das genau drei gleich große Teile? Dann wurde geschnitten. Dann kamen meine Fragen: „Zeigt einen Teil der Banane in die Höhe. Wie groß ist er?“ „Ein Drittel“. „Zeigt mir zwei Drittel, zeigt mir drei Drittel. Wie viele Drittel ergeben die ganze Banane?“
Anschließend sollte jedes Drittel halbiert werden. „Wie viele Teile haben wir nun insgesamt?“ „Sechs“. „Zeigt einen Teil der Banane. Wie groß ist er?“ „Ein Sechstel“. „Zeigt mir zwei Sechstel, zeigt mir drei Sechstel.“ Dann kam eine Frage für Pfiffige: „Legt drei Sechstel zusammen. Wer weiß, was die drei Sechstel auch noch sind?“ Einige kommen drauf und man merkt ihnen die Erkenntnisfreude an. Die Augen leuchten und sie wollen unbedingt drangenommen werden. Ich warte gerne absichtlich ein bisschen und wiederhole die Frage nochmal, bis bei immer mehr Kindern der Groschen fällt. „Ein Halb!“ Jetzt für alle: „Stimmt das? Legt die anderen drei auch zusammen.“ Ja, es ist ganz offensichtlich. Drei Sechstel und ein Halb sind das Gleiche. „Zeigt mir vier Sechstel, dann fünf Sechstel.“ Und am Ende wieder die Frage: „Wie viele Sechstel hat die ganze Banane?“ „Sechs Sechstel.“
Auf der nächsten Epochenheftseite bekamen die Kinder nun die Aufgabe unsere Teilung der Banane wie beim Stock festzuhalten und zu beschriften. Das können die meisten Kinder alleine. Ich habe es etwas zeitverzögert an der Tafel mitgemacht, sodass unsichere Kinder schauen konnten.
Jetzt durfte die Banane gegessen werden!
Hausaufgabe: Bringe morgen einen Apfel, ein Messer und ein Frühstücksbrettchen mit.
3. Tag
Heute sollten die Kinder die einzelnen Arbeitsschritte aus diesem Übungsblatt entnehmen. Das Blatt beschreibt die gewohnten Abläufe der ersten beiden Tage, diesmal mit einem Apfel. Geübt wird, Arbeitsschritte einem Text und nicht nur den Worten des Lehrers entnehmen zu können. So sagte ich nur zu den Kindern: „Ich bin mal gespannt, ob Ihr die Aufgaben auf dem Blatt ganz ohne mich lösen könnt.“ Wer Fragen hatte, konnte zu mir nach vorne an meinen Tisch kommen. Am Ende verglichen wir die Ergebnisse.
Hausaufgabe: Bringe morgen etwas mit, was du gerne isst und das man gut teilen kann. Packe wiederum ein Frühstücksbrettchen und ein Messer ein.
Letzter praktischer Tag
Es war interessant, was die Kinder so mitbrachten: Eine Pizza, verschiedene Würste, einen Pfirsich, einen Kuchen und ganz viele Schokoladentafeln.
Heute haben wir folgenden Weg beschritten: Erst halbieren, dann nochmals halbieren und nochmals halbieren. Wer wollte und konnte, durfte nochmals halbieren. So kamen wir zu Achtel bzw. Sechzehntel. Der Weg sollte anschließend wie beim Stock und der Banane im Heft allein dokumentiert werden.
Fazit
Mit der Bruchrechnung wird ein neues Denken innerhalb der Mathematik begonnen. Es ist ein Rechnen in Verhältnissen – das Verhältnis einer bestimmten Zahl von den Teilen zu einem Ganzen. Daher kann man Brüche auch nicht mehr so einfach einordnen wie ganze Zahlen. Oder wie schnell finden Sie heraus, was größer ist: 3/7 oder 4/9?
Um die Grundlagen für das Rechnen in Verhältnissen zu legen, müssen diese langsam und anschaulich aufgebaut werden. Es muss ein Gefühl für den Bruch entstehen. Dafür fand ich den beschriebenen Weg als sehr geeignet. Selbstverständlich kann man ihn nach Belieben variieren und verändern. Ab dem 3. Tag kann man sehr gut weiteres Anschauungsmaterial hinzunehmen wie z.B. „Kopiervorlage: Kreise mit 1 – 12 Segmenten“. Auch magnetische Bruchstücke von Kreisen und Vierecken für die Tafel sind als weiterführendes Material überaus sinnvoll.

