Epochenaufbau
Ein Beitrag von Franka Paul
Vorbemerkung
In dieser Epoche geht es darum, den Schüler*innen vom intuitiven zeichnerischen Tätigsein (Formenzeichnen, Klasse 1-4) hin zum gedanklichen Durchdringen einfacher geometrischer Formen (Freihandgeometrie, Klasse 5) zu begleiten und anzuregen. Alle Schüler*innen erhalten durch praktische Übungen und eigenes Ausprobieren die Möglichkeit, Sicherheit beim Zeichnen der Formen (Stiftführung, Proportionen der Formen, Platzierung auf dem Papier, farbliche Gestaltung) sowie beim Definieren von geometrischen Grundbegriffen zu gewinnen. Methodisch gehe ich nach dem Prinzip des individualisierten, kooperativen und selbstverantwortlichen Lernens vor. Das bedeutet, dass ich die Schüler*innen möglichst viel individuell und selbständig erfahren und erforschen lasse und ihnen die Möglichkeit gebe, sich untereinander auszutauschen, zu inspirieren und zu helfen. So können sie einen individuellen, intrinsisch motivierten Zugang zum Thema finden und eigene Erkentnisse gewinnen.
Epochenaufbau
1. Schritt: Die Bewegungsqualitäten Gehen und Drehen erfahrbar machen
Bevor man verschiedene Formen aufgrund ihrer jeweiligen Eigenschaften definiert und voneinander unterscheidet, lässt sich die Verschiedenartigkeit konkret erlebbar machen, wenn auf die beiden Bewegungsqualitäten des Gehens und des Drehens geachtet wird: Laufen wir einen Kreis im Raum, schreiten wir in gleichem Maße fort wie wir uns um die eigene Achse drehen. Wir können dies verdeutlichen, indem wir beim Gehen auf der Kreislinie einen Stab am nach vorne ausgestreckten Arm halten und beobachten, wie dessen Spitze die Richtung ändert. Auch können wir uns die Körperansicht des Gehenden vergegenwärtigen: Wir sehen ihn im Laufe eines Kreises von allen Seiten. Das anschließende Zeichnen sah so aus (für jeden Schritt des Gehenden auf der Kreislinie machten wir einen zarten Punkt, dann zeichneten wir den Stab ein, wobei wir ihn nach hinten verlängerten und damit auch die Gegenlaufrichtung im Kreis abbildeten):
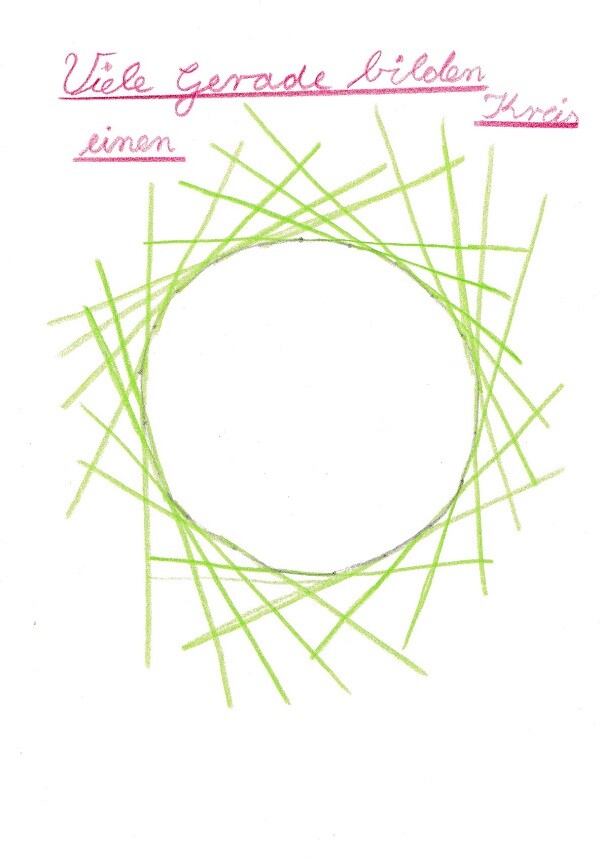
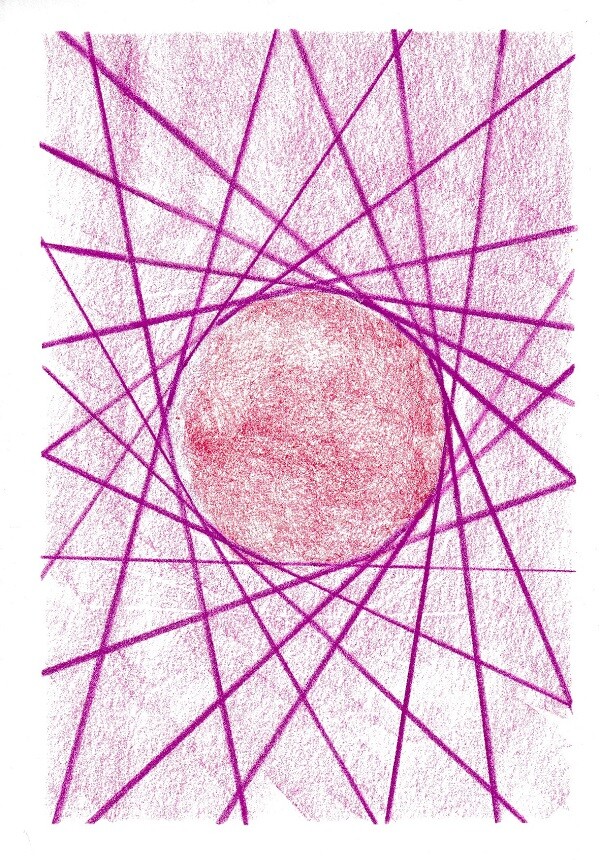
Am Folgetag liefen einzelne Schüler*innen auf diese Weise wieder einen Kreis. Wenn nun die Aufgabe gestellt wird, an zwei gegenüberliegenden Stellen stärkere Drehungen zu vollziehen, entsteht eine Ellipse. Das beobachteten wir wiederum am Stab, der auf den Längsseiten der Ellipse kaum, an ihren Enden aber sehr stark die Richtung ändert. Das gleichmäßige Fortschreiten und Drehen im Kreis verändert sich zu einem Rhythmus in der Ellipse.

Auch Dreieck und Quadrat untersuchten wir auf dieses beiden Bewegungsqualitäten hin. Die Schüler*innen konnten erleben, dass an den Eckpunkten der Drei- und Vierecke keinerlei Fortbewegung, wohl aber eine starke Drehung stattfindet. Umgekehrt findet beim Entlanggehen der Seiten keinerlei Drehung statt. Die Schüler*innen zeichneten intuitiv gleichseitige Dreiecke und Quadrate, die wir auch so benannten.

Um verschiedene Dreiecke und Vierecke zu erhalten, kann nun mit der Länge des Gehens und der Weite des Drehens gespielt werden, auch ganz praktisch bewegt im Raum oder gleich auf dem Papier. So entstehen "geduckte" oder "gestreckte" Dreiecke und unterschiedlich hohe oder breite Rechtecke.
Wir hatten nun durch die Bewegung im Raum und das Zeichnen auf dem Papier erlebt, dass sich die Grundformen Kreis, Ellipse, Dreieck und Viereck durch das jeweils unterschiedliche Verhältnis von Gehen und Drehen voneinander unterscheiden und dass bei Varianten der selben Grundform Längen und Weiten (später: Winkel) eine Rolle spielen. Diese Erfahrungen haben wir immer wieder besprochen und reflektiert.
Die Hausaufgaben waren sehr frei gestaltet. Jeden Tag ging es darum, aus der Grundform, die wir im Unterricht untersucht hatten, eine eigene Komposition zu gestalten. Es entstanden sehr individuelle und meistens sehr sorgsam gezeichnete Formen, die wir jeden Tag in die Mitte des Klassenraums legten und sie gemeinsam betrachteten, würdigten und daran interessante Entdeckungen machten.



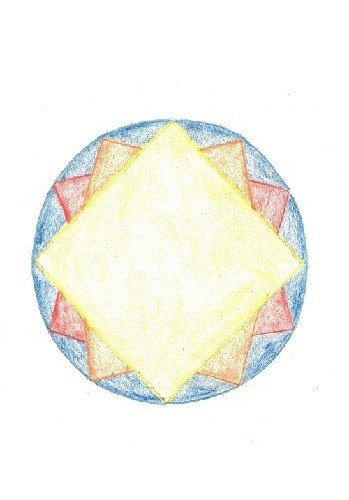

2. Schritt: Durch exakte Sprachverwendung ein Gespür für Definitionen erhalten
Etwa in der zweiten Woche begannen wir den Unterricht mit Zeichendiktaten. Dabei machten die Schüler*innen die Erfahrung, dass jede Form ihre ganz eigene Beschreibung, ihre eigene Definition hat, die sie von allen anderen Formen unterscheidet.
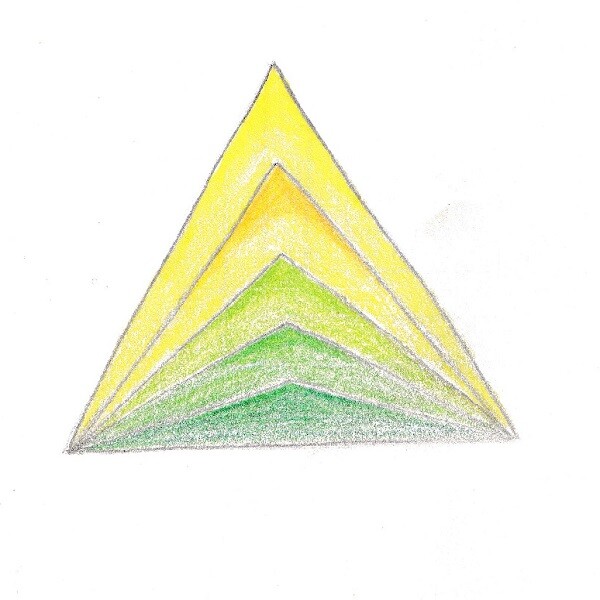
- Zeichnet in ein gleichseitiges Dreieck weitere Dreiecke hinein, deren obere Spitze sich senkt. Die waagerechte Seite der Dreiecke bleibt dabei gleich.
- Zeichnet um ein gleichseitiges Dreieck herum weitere Dreiecke, deren Spitze sich hebt. Die waagerechte Seite der Dreiecke bleibt dabei gleich.
Die Skizzen wurden als Hausaufgabe farbig ausgestaltet.

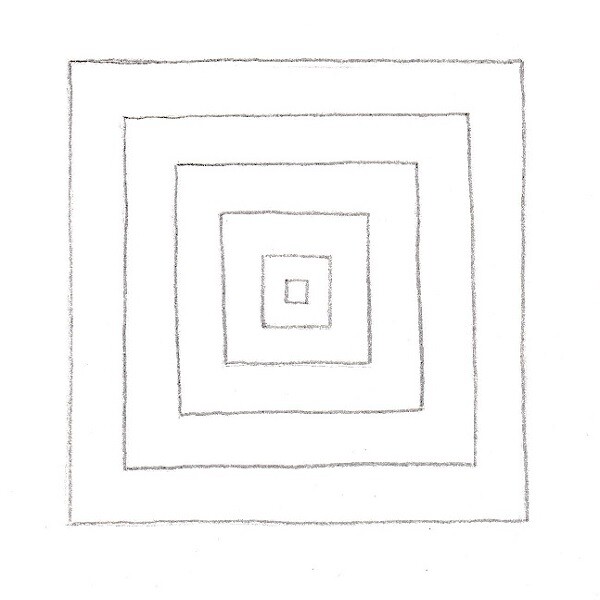
- Zeichnet in ein Quadrat weitere, kleiner werdende Quadrate hinein, die alle den gleichen Mittelpunkt haben.
- Zeichnet in ein Quadrat weitere, kleiner werdende Quadrate hinein, die alle einen gemeinsamen Eckpunkt haben.

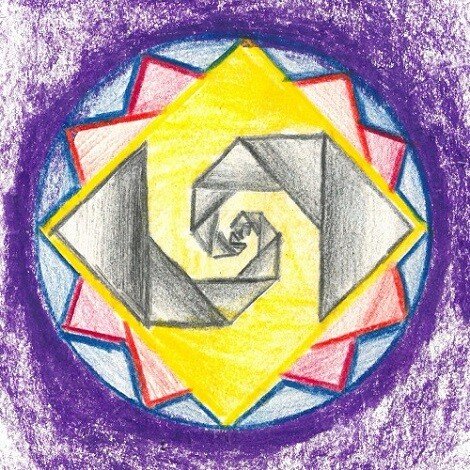
Als Hausaufgaben entstanden wieder individuelle Kompositionen. Dazu kamen Fünfecke und Fünfsterne, die wiederum den Umgang mit Dreiecken und Vierecken / Viersternen inspirierten:



3. Schritt: Das Grad - ein Himmelsmaß
Beim Ablaufen einer Kreislinie war deutlich geworden, dass sich der Gehende dabei ein Mal um sich selbst dreht. Wir kennen das Drehen um die eigene Achse noch aus der Heimat- und Himmelskunde: Dort hatten wir den Lauf der Sonne mit ausgestrecktem Arm nachgezeichnet, von ihrem Aufgang im Osten, über ihren Zenit im Süden bis zu ihrem Untergang im Westen und, unsichtbar für uns, ihren Weitergang im Norden. Diese Erfahrung können wir zum Ausgangspunkt für folgende Erzählung nehmen, die die Beobachtung des Nachthimmels betrifft: "Blickt man nämlich jede Nacht zur gleichen Zeit in die gleiche Richtung - zum Beispiel genau nach Süden - , dann sieht man, dass die gleichen Sterne jeden Tag etwa um vier Minuten früher in dieser Richtung ankommen. Nach etwa 360 Tagen (genauer nach 365 1/4 Tagen), also nach einem Jahr, kommen die gleichen Sterne zur gleichen Zeit wieder in die Beobachtungsrichtung. Diese tägliche Verschiebung haben die Alten als Maß für das Drehen gewählt, und zwar haben sie, da sich mit 360 leichter rechnen lässt als mit 365 1/4, den 1/360 Teil der vollen Drehung als Einheit für die Winkelmessung gewählt. Diese Einheit bezeichnet man als 1 Grad und schreibt 1°. Während also das Maß für die Länge (ein Meter, ein Yard oder was auch immer) von Gehen auf der Erde genommen wurde, stammt das Maß für das Drehen vom Himmel. Es ist ein Himmelsmaß." (In: Schuberth: Der Geometrie-Unterricht..., S. 18). Im Epochenheft illustrierten wir das folgendermaßen:

In der folgenden Tagen machten wir verschiedene Übungen zu den unterschiedlichen Winkeln:
- Sich mit dem eigenen Körper um 360°, um 180°, um 90° und um 45° Grad drehen.
- Zwischen Arm und Oberkörper verschiedene Winkel bilden.
- Zwischen Ober- und Unterarm verschiedene Winkel bilden.
- Zwei Kinder laufen in einem bestimmten Winkel vom gleichen Punkt aus in zwei verschiedene Richtungen.
- Verschiedene Winkel im Klassenraum finden.
Es ging also nicht darum, einen bestimmten Winkelgrad abzubilden oder zu konstruieren, sondern die grundlegenden Winkel in ihrer Unterschiedlichkeit mit dem Auge voneinander unterscheiden zu lernen (s. nächstes Bild).
Manche Kinder denken bei Winkeln ans Buchrechnen und die Aufteilung einer Kreisfläche in Segmente. Die verschiedenen Winkel-Übungen machen deutlich: Winkel sind von Flächen oder Raumgrößen unabhängig.

4. Schritt: Die wichtigsten Eigenschaften der Vierecke
Nun hatten wir die Voraussetzungen für das geometrische Denken und Definieren geschaffen und erprobten dies, indem wir die wichtigsten Eigenschaften der Vierecke bestimmten.
Neu hinzu kam dabei das Bestimmen der Spiegelachsen, das einige Vorstellungskraft erfordert und machen Schüler herausforderte. Beim Parallelogramm beispielsweise gab es eine Diskussion darüber, ob dieses wirklich keine Spiegelachse habe. Der Beweis brachte schließlich ein ausgeschnittener Parallelogramm, das in alle möglichen Richtungen gefaltet wurde und tatsächlich nirgendwo mit seinen Hälften exakt aufeinanderpasste.
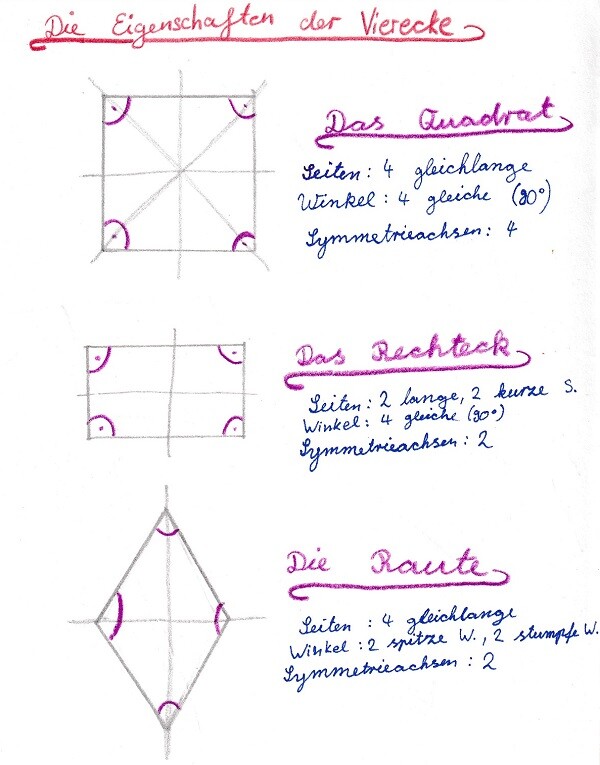
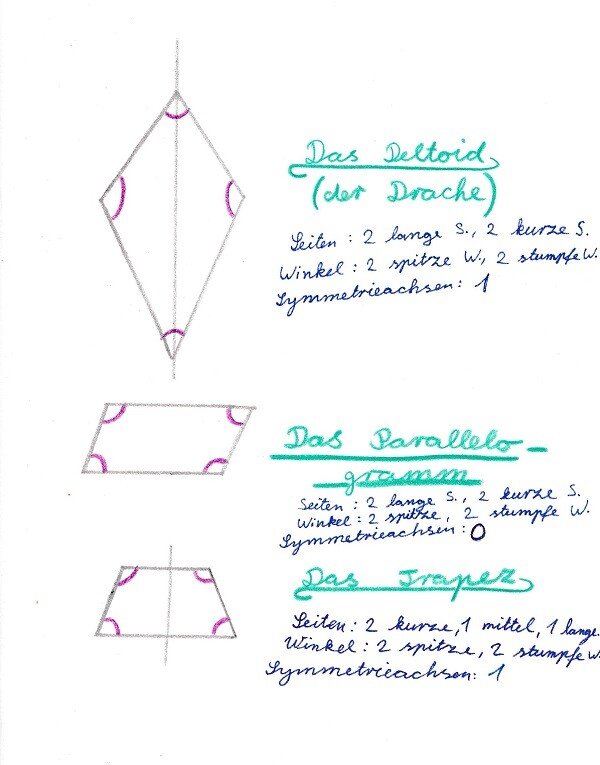
Übersicht der Fachbegriffe
- Waagerechte; Senkrechte (das Lot); Diagonale (verbindet die gegenüberliegenden Ecken einer Form)
- Kreis, Ellipse, gleichseitiges Dreieck, Quadrat
- Vierecke: das Rechteck, das Quadrat, die Raute, der Drache (das Deltoid), das Parallelogramm, das gleichschenklige Trapez
- Winkel, Schenkel des Winkels
- spitzer Winkel, rechter Winkel, stumpfer Winkel, gestreckter Winkel, überstreckter Winkel, voller Winkel
- Symmetrieachse (Spiegelachse)
Rückblick
Es war eine Epoche mit hoher Schüleraktivität durch konzentriertes Zeichnen, durch waches und interessiertes Wahrnehmen und Beschreiben der Schülerarbeiten und durch freudige Mitteilung gewonnener Erkenntnisse. Es empfielt sich ein rasches Voranschreiten durch die oben beschriebenen Themengebiete, so dass in der letzen Woche das Erarbeitete weiter geübt und damit vertieft werden kann.
Literatur
Dieser Epochenaufbau orientiert sich am Buch von Ernst Schuberth Der Geometrie-Unterricht an Waldorfschulen. Band2: Vergleichende Formenlehre und geometrische Grundkonstruktionen in den Klassen 4 und 5, Verlag Freies Geistesleben.

