Alle 4 Grundrechenarten schon im ersten Schuljahr?
Ein Beitrag von Herrn Häberlen (Förderlehrer an der Tübinger Freien Waldorfschule)
Im Gegensatz zu den staatlichen Schulen, in denen die Schüler frühestens in der zweiten Klasse das Multiplizieren und Dividieren als Rechenarten kennen lernen, werden in der Waldorfschule auf Empfehlung Rudolf Steiners schon in der ersten Klasse ziemlich rasch hintereinander alle vier Grundrechenarten eingeführt, oder anders gesagt, sie werden gar nicht so scharf voneinander getrennt. Ist das nicht eine maßlose Überforderung der Kinder?
Nun, wenn man meint, damit schon so abstrakte Zahlenrechnungen wie 12 : 4 = 3 oder 20 : 4 = 5 lösen zu müssen, wäre dies sicher der Fall. Was Rudolf Steiner damit gemeint hat, wenn er wollte, dass die 4 Grundrechenarten fast gleichzeitig eingeführt werden sollten, kann man nur verstehen, wenn man weiß, dass er bei der Einführung des Rechnens nicht von den einzelnen Elementen ausgeht, sondern von dem Ganzen einer bestimmten Menge, die dann in der vielfältigsten Weise aufgegliedert werden kann. Man könnte auch sagen: Am Anfang steht nicht die Aufgabe, sondern das Ergebnis, und wir suchen dazu möglichst viele passende Aufgaben.
Im ersten Falle wird das Kind nämlich auf eine einzige richtige Lösung eingeengt, während es im zweiten die Freiheit erlebt, aus ganz verschiedenen Möglichkeiten eine auszuwählen, und in seiner Phantasie in ganz anderer Weise angeregt wird.
Machen wir uns dies an einem Beispiel klar: Es ist vielleicht gerade Herbst und wir rechnen in der 1. Klasse mit Äpfeln. Dann würde die Aufgabe nicht lauten: „Du hast 5 Äpfel und bekommst noch 3 dazu," sondern so: „Hier hast du 8 Äpfel, wie könntest du daraus 2 oder 3 oder noch mehr Häufchen machen?" Dabei wären zum Beispiel folgende Lösungen möglich, wobei die Aufzählung noch lange nicht vollständig ist:
1+7; 4 + 4; 3 + 3 + 2; 2 + 4 + 2; 5 + 2 + 1; 1+3 + 4; 2 + 2 + 2 + 2; 1+3 + 3 + 1; 3 + 5; 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1; 2 + 2 + 2 + 1 + 1
Unter den vielen Möglichkeiten der Aufteilung gibt es nun auch solche, bei denen die gleiche Zahl mehrmals vorkommt:
4 + 4; 3 + 3 + 2; 2 + 4 + 2; 2 + 2 + 2 + 1 + 1; 1 + 3 + 3 + 1; 2 + 2 + 2 + 2; 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
Hier kann ich nun zum Beispiel bei 2 + 2 + 2 + 2 das Kind fragen: „Wie oft hast du 2 Äpfel bekommen?" - „Viermal!" Und schon sind wir mitten im Multiplizieren, aber auch im Dividieren: 8 Äpfel kann ich in vier Zweierhäufchen aufteilen.
Eine andere Aufgabe wäre: „Mache aus 8 Äpfeln zwei gleich große Häufchen." Dann hat jedes 4 Äpfel. Solche Aufgaben sollte man aber nicht schon in die übliche Form: 8 : 2 = 4 bringen, sondern viel eher so notieren:

Das echte Verteilen (im Gegensatz zum Aufteilen) könnte so aussehen:
Verteile 8 Äpfel auf 4 Kinder
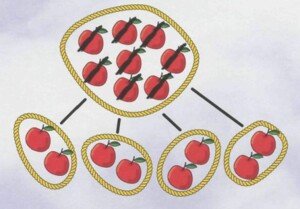
Später, vielleicht erst in der 2. Klasse, kann dann die Schreibweise auch so sein:
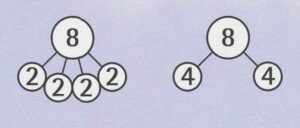
Das Prinzip, vom Ganzen auszugehen und dann verschiedene Aufteilungen zu suchen, kann man in ganz entsprechender Weise in den höheren Klassen wieder anwenden, wenn man zum Beispiel beim Üben des Einmaleins nicht so sehr fragt, was 6 • 3 oder 7 • 4 ist, sondern wenn man eine bestimmte Zahl nimmt und möglichst viele Malaufgaben dazu sucht:
36 = 1 • 36; 2 • 18; 3 • 12; 4 • 9; 6 • 6; 9 • 4; 12 • 3; 18 • 2; 36 • 1
Hier den richtigen Überblick zu haben ist zum Beispiel in der 7. oder 8. Klasse beim Umwandeln von algebraischen Ausdrücken wichtig:
x²+ 13x + 36 = (x + ?)(x + ?)
Ich muss mich hier fragen, welche beiden Zahlen miteinander multipliziert 36 und miteinander addiert 13 ergeben.
x² + 13x + 36 = (x + 9) (x + 4)
Unter den verschiedenen Aufteilungsmöglichkeiten der 36 gibt es nun wieder eine, bei der die beiden Zahlen gleich sind: 6 • 6. Und auch hier können wir uns eine einfachere Schreibweise überlegen.
So kommen wir zum Potenzieren: 36 = 6² . Wenn wir die Teilfaktoren weiter aufteilen, kommen wir auch zu Aufgaben wie 32 = 2 • 2 • 2 • 2 • 2 oder 32 = 25 Wie beim Multiplizieren haben wir gleiche Glieder, aber im Gegensatz zu diesem werden sie nicht addiert, sondern multipliziert.
Dies kann uns zu der schönen Sage aus dem alten Indien führen, die uns erzählt, wie der Erfinder des Schachspiels vom König eine Belohnung versprochen bekam und er sich „nur" wünschte, auf das erste Feld des Schachbretts ein Reiskorn und dann auf die nächsten jeweils die doppelte Anzahl zu bekommen, also 1; 2; 4; 8; und so weiter. Der König, der dies zunächst als eine geringe Belohnung ansah, musste bald einsehen, dass der Wunsch unerfüllbar war. Wer es nicht glaubt, möge nur einmal die Anzahl der Körner auf dem letzten Feld ausrechnen, nämlich 263. Er kann dabei ruhig 210 = 1024 auf 1000 abrunden und dann weiterrechnen.
In der Oberstufe werden dann die Schüler erfahren, wie diese so genannten Zweierpotenzen die Grundlage für sämtliche Leistungen eines Computers sind.
Mein Anliegen war, beispielhaft aufzuzeigen, wie Zusammenhänge bestehen von der allerersten Einführung des Rechnens bis hinauf in die Mathematik der Oberstufe und wie fruchtbar dabei der Ansatz der Waldorfschule sein kann, nicht von den Einzelheiten, sondern von einem Ganzen auszugehen.
K. Häberlen (Förderlehrer)

