Feldmessen mit dem Messtisch (10. Klasse)
Ein Beitrag von Peter Clementsen (Michael Schule Hamburg-Harburg)

Angeregt und ermutigt durch den Artikel von Günter Kampffmeyer in der Erziehungskunst 03/08 beschloss ich im Frühjahr, die Feldmess-Epoche an der Michael Schule (für heilende Erziehung) in Hamburg-Harburg nicht wie gewohnt mit Theodolithen, sondern mit Messtischen zu versuchen. Nicht die Beschaffung der Messgeräte sprach dafür (dabei wurden wir großzügig von der Raphael-Schule unterstützt), sondern die Durchschaubarkeit des Verfahrens - sie schien mir für unsere Schüler wichtig zu sein.
Mit Hilfe der „Anleitung zum Feldmesspraktikum der 10. Klasse" vom Kasseler Seminar machte ich mich mit dem Verfahren vertraut und vereinfachte es soweit, dass jede Gruppe in zwölf Tagen ihr Gebiet ausmessen und zeichnen konnten, so dass noch eine gemeinsame Karte aus den drei Gebieten entstehen konnte.
Weil das Vorgehen erfolgreich war, möchte ich es kurz vorstellen:
Zuerst wird das Gebiet durch Fluchtstäbe markiert: Jede Ecke bekommt einen Stab, der nummeriert wird. Dann suchen wir in der Mitte des Feldes zwei Punkte, von denen alle Stäbe zu sehen sind. Die beiden Punkte sollen möglichst weit auseinander liegen und es dürfen keine Stäbe in der Flucht der Verbindungslinie stehen. Je näher die Punkte an dieser Flucht stehen, umso größer ist der unvermeidliche Messfehler.
Sich für diesen Teil der Arbeit zu wenig Zeit zu lassen, wäre ein Fehler. Schon in der schulischen Vorbereitung können die Schüler die Bedeutung einer guten Position der Messtische schätzen lernen und dann im Praktikum gemeinsam nach der besten Lösung suchen.
Von den Nachbargebieten müssen mindestens zwei Stäbe ebenfalls zu sehen sein, damit der Anschluss in der großen Zeichnung möglich ist.
Dann wird der Messtisch auf Position A aufgestellt. Ein vorbereitetes DIN-A3-Blatt zur „Messtisch-Aufnahme" braucht mindestens eine gut sichtbare Linie, denn auf beiden Positionen müssen die Blätter möglichst genau „eingenordet" sein, sie dürfen nicht gegeneinander verdreht sein.
Das Blatt ist natürlich beschriftet:
Messtisch-Aufnahme, Position:__ , Gebiet:__ , Datum:__, Gruppe:__ , Protokollant:__
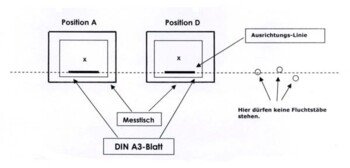
Das x kennzeichnet die Mitte des Blattes. Durch diesen Punkt müssen alle Linien gehen, die nun gezeichnet werden. Wenn der Tisch einigermaßen waagerecht und so fest steht, dass er sich während der nun folgenden Arbeit nicht dreht, wird der erste Fluchtstab anvisiert und die genaue Richtung als Linie (durch x) gezeichnet. Dafür kann ein Diopterlinial verwendet werden, also ein Lineal mit Kimme und Korn zum Anvisieren der Stäbe. Es gibt auch aufwendige Geräte, sogenannte Kipp-Regale, die noch ein Fernrohr mit Fadenkreuz integriert haben, mit denen sich genauer arbeiten lässt. So eines zu bekommen, wäre aber ein Glücksfall (in diesem Fall durch einen befreundeten Berufsschullehrer).Auf das Blatt können nun alle Fluchtstab-Richtungen von dieser Position aus eingezeichnet werden. Die Linien müssen natürlich eindeutig gekennzeichnet sein. Der Protokollant hat hier eine verantwortungsvolle Aufgabe. Er ist es auch, der später die Übertragung ausführt.
Die genaue Ausrichtung der Messtische und die Standfestigkeit der Tische entscheiden über die Qualität der Messung. Wenn der Tisch während der Messung auch nur wenig gedreht wird, muss mit einem neuen Blatt noch einmal begonnen werden.
Nachdem alle Fluchtstäbe aufgenommen sind, wird der Messtisch an die nächste Position gestellt und von dort auf einem neuen Blatt wieder alle Fluchtstab-Richtungen eingezeichnet. Man erhält zwei Blätter. Der Abstand der beiden Positionen wird mit dem Maßband gemessen.

Bei der Auswertung werden nun diese Linien auf ein größeres Blatt übertragen. Zuerst von Position A: Das Aufnahme-Blatt wird etwa in die Mitte des großen Blattes gelegt und mit Kreppband fixiert; seine Position wird genau auf dem großen Blatt gekennzeichnet. Mit einem langen Lineal werden die Linien verlängert; nachdem das Aufnahme-Blatt entfernt wurde, werden sie auf dem großen Blatt durchgezogen, natürlich mit Beschriftung, am besten an beiden Enden der Linien.
Dann von Position D. Dieses Blatt wird jetzt genau so weit neben der Position des ersten Blattes fixiert, wie es dem Abstand im gewählten Maßstab entspricht: Waren die Messtische 210 m auseinander und der Maßstab soll 1:1000 sein, wird das D-Blatt 21 cm rechts von der Position des A-Blattes befestigt. Wieder werden die Linien verlängert, beschriftet und durchgezogen.
Es entsteht ein Gewirr von Linien, eine Herausforderung an die Konzentrationsfähigkeit. Dort, wo die beiden Linien nach F1 sich schneiden, liegt der Fluchtpunkt F1 in der Zeichnung, ebenso F2, F3 usw. Alle Schnittpunkte werden eingekreist und beschriftet.
Ist diese Arbeit vollbracht, brauchen nur noch - entweder mit Hilfe von Transparentpapier oder mit einer Nadel - die maßstabgetreuen Fluchtpunkte auf ein Blatt übertragen zu werden. Die anschließende Kleinvermessung, die der Zeichnung erst den Inhalt gibt, wird hier nicht beschrieben.
Auf diese Art ist ohne Rechnung eine maßstäbliche Darstellung des Polygonzuges gelungen, der durch die Fluchtstäbe gebildet wird.
Diese Messung kann genau genug sein, um eine Karte im Maßstab 1:1000 und wohl auch darunter zeichnen zu können. Wichtig sind ein möglichst großer Abstand der Positionen, die genaue Ausrichtung der Tische und der möglichst große Abstand der Messpunkte von der Flucht der Verbindungslinie der beiden Positionen, weil sonst die Linien auf beiden Blättern fast parallel verlaufen.
Wie genau die Messungen waren, ob sie überhaupt brauchbar sind, lässt sich so allerdings erst am Ende der Arbeit überprüfen: Die Abstände der einzelnen Fluchtpunkte in der Zeichnung und in der Realität werden verglichen.
Weil die Schüler schon im vorbereitenden Matheunterricht lernten, dass Messungen nie ganz genau sind, haben wir folgendes getan:
Eine dritte Position C des Messtisches in der Verbindungslinie zwischen A und D führt bei der Übertragung auf das große Blatt zu zwei weiteren Schnittpunkten je Fluchtpunkt: A schneidet C und C schneidet D. Die drei Schnittpunkte werden nur in Ausnahmefällen übereinander liegen - eben weil keine Messung ganz genau sein kann. Wenn die drei Schnittpunkte aber zu weit auseinander liegen, weiß man, dass (mindestens) eine der drei Messungen zu ungenau war. Welche das ist, weiß man allerdings nicht.
Darum haben wir von vier Positionen aus die Richtungen der Fluchtstäbe gezeichnet, von A, B, C und D. Nun gibt es sechs Schnittpunkte: meistens drei Punkte, die dicht zusammen liegen und drei, die von diesen weiter entfernt sind: Sie gehören zur ungenauesten Messung.
Es ergibt sich damit natürlich ein noch größeres Gewirr von Linien, doch die Schüler haben den Vorteil dieser vier Messungen verstanden und die erfolgreiche Entdeckung der (nun sechs) Schnittpunkte, die dann auch noch zusammen passen (oder auch mal nicht, wenn der Winkel zu spitz war, weil die Messpunkte zu nah an der Verbindungsgraden lagen), sind ein Lohn für genaues Messen und konzentriertes Auswerten. Die Erfahrung hat gezeigt, dass auf diese Art noch genug Zeit blieb, um jedem Schüler die Gelegenheit zu geben, seine eigene Gesamtkarte zu zeichnen.
Durch die Anschaulichkeit des Verfahrens scheint mir die Vermessung mit Messtischen eine empfehlenswerte Alternative zumindest für heilpädagogische Schulen zu sein.
Gerne dürfen Sie mich bei Rückfragen kontaktieren.
Peter Clementsen
E-mail: Peter.Clementsen@t-online.de

