Primzahlen - Sieb des Erathostenes
Ein Beitrag von Christian Imann (Freie Waldorfschule Emmendingen)
Erathostenes (ca.300v.Chr.), griechischer Mathematiker, erdachte ein Verfahren, um systematisch Primzahlen aus einer Liste der natürlichen Zahlen zu erzeugen.
Eine Primzahl ist eine Zahl, die ausschließlich durch 1 und sich selbst teilbar ist.
Erathostenes` Sieb funktioniert wie folgt:
- Zu Beginn schreibt man die Reihen der natürlichen Zahlen zum Beispiel von 1 bis 100 in zehn Zehner-Spalten nebeneinander.
Für ganz Verwegene hier eine Tabelle der Zahlen 1 – 1000:
Zum Download: Sieb des Erathostenes 1 - 1000 - Die 1 streicht man durch, weil sie ist noch keine Primzahl ist.
- Jetzt „sucht“ man die erste undurchstrichene Zahl. Das ist natürlich die 2. Sie ist die erste Primzahl und wird nicht durchgestrichen. Dafür beginnt man aber jetzt das ganze System der Reihe nach durchzugehen und alle Vielfachen der 2 durchzustreichen: 4, 6, 8, … Ist man damit fertig, so wendet man wiederum seinen Blick an den Anfang und sucht die nächste undurchstrichene Zahl.
- Das ist die 3 (also Primzahl, wird nicht durchgestrichen). Alle Vielfachen der 3 werden durchgestrichen. Die nächste undurchstrichene Zahl ist die 5 (die 4 war ein Vielfaches der 2).
- Die 5 bleibt undurchstrichen (Primzahl), alle Vielfachen werden durchgestrichen …
- …. hat man alle Reihen durch, sind letztlich alle ungestrichenen Zahlen Primzahlen.
Will man dasselbe Prinzip des Siebes vom Blatt in den bewegten Raum verlegen, so kann man Folgendes versuchen. Ich habe es mit einer Gruppengröße von 19 Schülern probiert und mit ein wenig Übung und viel Konzentration funktioniert es:
- Die Klasse stellt sich in einem Kreis auf. Jeder Schüler legt zu seinen Füßen Blatt, um den Standort zu fixieren.
- Ein Schüler tritt aus dem Kreis heraus, er hat die Zahl 1 und erhält im Folgenden die Aufgabe des Abzählers. Langsam um den Kreis herumgehend hält er kurz bei seinem linken Nachbarn inne und betitelt ihn laut als „Zwei“.
- Die 2 ist von niemandem ein Vielfaches (also Primzahl). Daher muss sie sich der 1 sofort anschließen. Dieses Schicksal ereilen für das weitere Spiel alle Primzahlen. Es ergibt sich dadurch eine Primzahlenschlange, die immer länger wird, je mehr man fortschreitet. Alle Primzahlenschüler haben die Aufgabe, innerlich abzuzählen – von der „Eins“ bis zu sich selbst – dann haben sie im Kreis ein Vielfaches von sich gegenüber. Ihm sagen sie dann: „Vielfaches“
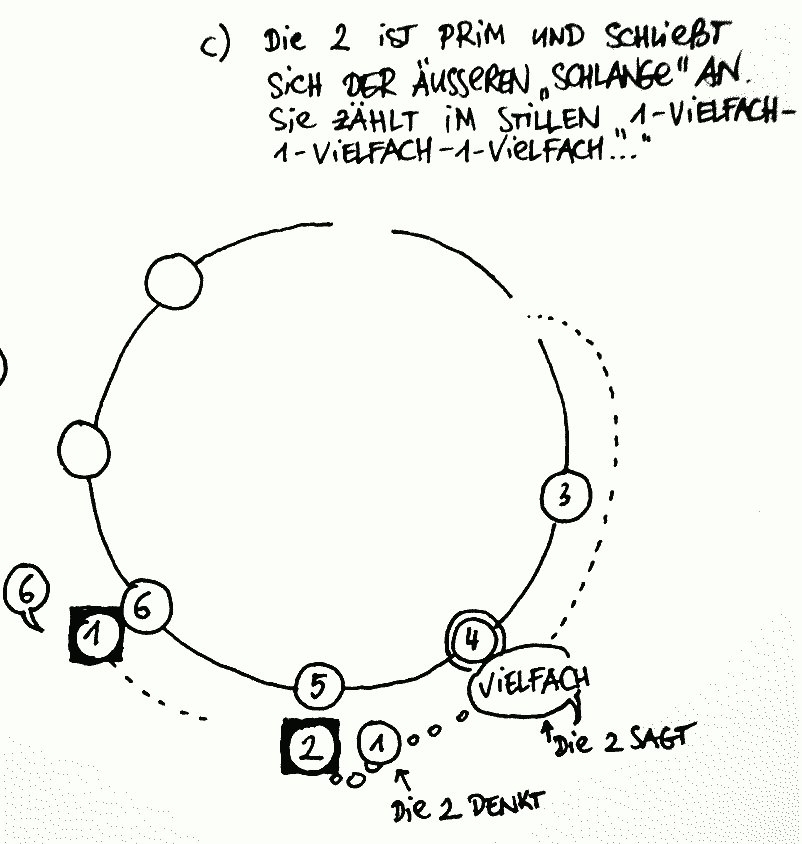
- Ist die Schlange an einem Schüler im Kreis vorbeigegangen und es hat keiner der Primzahlen zu ihm „Vielfaches“ gesagt, so ist er selbst Primzahl und schließt sich dem Ende der Schlange sofort an.
- • Kommt die 1 zu ihrem ursprünglichen Platz zurück, so findet sie den eigenen und den von der 2 und 3 verlassen vor. Die 4 war im ersten Kreisumlauf ein Vielfaches - musste also stehen bleiben. Die Lücken bleiben vom Abzähler ungezählt, sodass die ursprüngliche 4 von der 1 bei z.B. 19 Schülern in die 20 umgetauft wird. So geht es Kreis um Kreis weiter, die Schlange wird immer größer und die Lücken im Kreis immer zahlreicher.
- Zum Schluss ist auch der Letzte aus dem inneren „Kreis" erlöst und geht in den äußeren Kreis der Schlange. Nun kann man schauen, ob alles gut funktioniert hat und verrät sich die gemerkten Zahlen, es sollte bestenfalls mit 1, 2, 3, 5, 7, 11, 13,... beginnen. Letztlich hat so jeder Schüler seine Primzahl gewonnen.
Dieses Spiel erfordert äußerste Wachheit und Konzentration. „Was war meine Zahl?", „Bin ich ein Vielfaches oder muss ich raus?" sind dabei die häufigsten Fragen. Es ist ausgesprochen wichtig, dass sich „Primzahlen“ immer an das Ende der Schlange anschließen und sich niemand dazwischen drängelt.
Falls Sie diese Idee ausprobieren wollen oder ausprobiert haben, so senden Sie mir doch eine Notiz an: imann@wds-emmendingen.de
oder nutzen Sie die Kommentarfunktion.
Viel Erfolg und gutes Gelingen
Christian Imann
(Mathematik Oberstufe)

