Dreieckstransversalen
Das Konstruieren macht den Menschen von klein auf Freude. Kaum dem Säuglingsalter entwachsen, konstruieren Kleinkinder mit großer Begeisterung aus ihren Bausteinen wackelige Türme. Wenn diese dann unter lautem Getöse zusammenstürzen, ist dies oft auch ein Grund zur Freude. Dann stehen die Steine wieder für neue Konstruktionsversuche zur Verfügung. Später werden Legosteine genommen. Und so mancher Hobbykeller beweist, dass auch im fortgeschrittenen Alter die Freude am Konstruieren nicht verloren geht.
Das Konstruieren von Dreiecken ist natürlich ganz anderer Art. Am Anfang sind die Aufgaben einfach zu überblicken. Später können sie sehr anspruchsvoll werden. Wichtig ist es, sich gleich zu Beginn das Erstellen einer Planfigur anzugewöhnen. Bevor man nun anfängt, sollte man nämlich den Weg der Konstruktion einmal gedanklich durchgegangen sein. Manchmal gibt es verschiedene Möglichkeiten zu beginnen. Später gibt es manchmal nur einen Weg, den man nehmen kann und dieser liegt noch nicht einmal auf der Hand.
Man erübt dabei ein konzentriert vorausschauendes Denken. Wenn man die Konzentration jedoch nicht lang genug zu halten vermag, so muss man erneut von vorn beginnen und die Konstruktion innerlich aufbauen. Auf der einen Seite kann der Moment einer erfolgreichen Konstruktion sehr beglücken, andererseits wird man frustriert sein, wenn man innerlich zu früh aussteigt und zu keiner Konstruktionsidee kommt.
Grundbegriffe eines Dreiecks:
Die Eckpunkte eines Dreiecks bezeichnet man mit den Großbuchstaben A, B und C. Unten links beginnt man mit A; dann geht man gegen den Uhrzeigersinn voran.
Die Seiten eines Dreiecks bezeichnet man mit den Kleinbuchstaben a, b und c. Seite a liegt gegenüber von Punkt A, Seite b liegt gegenüber von Punkt B und Seite c liegt gegenüber von Punkt C.
Die Winkel eines Dreiecks heißen α, β und γ. α liegt bei Punkt A, β bei Punkt B und γ bei Punkt C.
Die vier Grundkonstruktionen eines Dreiecks
1. Die Längen der drei Seiten sind gegeben.
Aufgabe:
Konstruiere ein Dreieck mit den Seitenlängen
a = 3 cm, b = 4 cm und c = 6 cm.
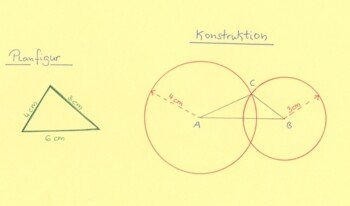
Konstruktionsplan:
Wir zeichnen zunächst die Seite c mit 6 cm. Wir erhalten somit A und B. Nun stellen wir unseren Zirkel auf 4 cm ein und schlagen einen Kreis um A. Anschließend schlagen wir einen zweiten Kreis um B mit dem Radius von 3 cm. Die Kreise schneiden sich an 2 Stellen. Nur diese beiden Schnittpunkte erfüllen gleichzeitig die oben genannten Seitenlängen. Entsprechend der positiven Laufrichtung des Dreiecks wählen wir den oberen aus und bezeichnen ihn mit C.
Es reicht anstelle eines ganzen Kreises auch ein Kreisausschnitt im Bereich des vermuteten Schnittpunktes.
Übungsaufgaben:
1. a = 5 cm, b = 6 cm; c = 4 cm
2. a = 3 cm, b =7 cm; c = 8 cm
3. a = 8 cm, b = 4 cm; c = 6 cm
4. a = 5 cm, b = 3 cm; c = 4 cm
5. a = 7 cm, b = 6 cm; c = 9 cm
6. a = 6 cm, b = 2 cm; c = 5 cm
7. a = 6 cm, b = 7 cm; c = 8 cm
8. a = 9 cm, b = 8 cm; c = 5 cm
9. a = 7 cm, b = 10 cm; c = 6 cm
2. Die Längen von zwei Seiten und die Größe des von ihnen eingeschlossenen Winkels sind gegeben.
Aufgabe:
Konstruiere ein Dreieck mit
a = 3 cm, c = 7 cm und β = 65°.
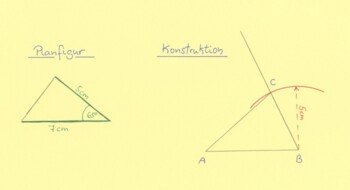
Konstruktionsplan:
Zunächst zeichnen wir die Seite c mit 7 cm und erhalten A und B. Anschließend nehmen wir das Geodreieck und messen bei β einen Winkel von 65° ab. Wir erhalten die Lage von der Seite a. Um die genaue Position von C zu finden, nehmen wir den Zirkel mit dem Radius von 3 cm und stechen ihn in B. Wir tragen auf a die 3 cm ab und erhalten C. Zuletzt werden die Punkte A und C miteinander verbunden.
Übungsaufgaben:
1. a = 3 cm; b = 4 cm; γ = 60°
2. a = 2 cm; b = 4 cm; γ = 120°
3. a = 3,2 cm; c = 5,5 cm; β = 35°
4. b = 4,8 cm; c = 2,9 cm; α = 75°
5. a = 7 cm; b = 7 cm; γ = 50°
6. a = 6 cm; c = 4,5 cm; β = 70°
7. b = 8 cm; c = 6 cm; α = 30°
8. a = 4,6 cm; b = 3,5 cm; γ = 100°
9. a = 5,9 cm; c = 8 cm; β = 27°
3. Die Länge einer Seite und die Größe zweier Winkel sind gegeben.
Diese dritte Grundkonstruktion umfasst zwei Fälle
1.) Beide Winkel liegen an der 2.) Einer der beiden Winkel
gegebenen Seite liegt gegenüber der angegebenen Seite
Aufgabe (1. Fall):
Konstruiere ein Dreieck mit
c = 6 cm, α = 50° und β = 30°.
Konstruktionsplan:
Zunächst zeichnen wir die Seite c mit 6 cm und erhalten A und B. Anschließend tragen wir die Winkel α und β ein. An der Stelle, wo sich die Seiten b und a schneiden, liegt der Punkt C. Diesen verbinden wir mit A und B.
Im 2. Fall müssen wir zunächst den 3. Winkel ausrechnen, um das Dreieck konstruieren zu können. Alles Winkel zusammen ergeben 180°. Ziehen wir die beiden gegebenen Winkel ab, so erhalten wir den fehlenden Winkel. Mit diesem Wissen konstruieren wir das Dreieck nun wie im 1. Fall.
Übungsaufgaben:
1. b = 5 cm; α = 40°; γ = 60°
2. c = 6 cm; β = 35°; γ = 55°
3. a = 5,6 cm; β = 25°; γ = 85°
4. a = 5 cm; α = 45°; γ = 85°
5. b = 6 cm; α = 60°; γ = 60°
6. c = 5 cm; α = 80°; γ = 45°
7. a = 4,8 cm; α = 75°; β = 35°
8. b = 3,6 cm; α = 110°; β = 25°
9. c = 3,8 cm; α = 65°; β = 48°
10. b = 7,2 cm; β = 45°; γ = 90°
4. Die Länge zweier Seiten und die Größe eines nicht von ihnen eingeschlossenen Winkels sind gegeben.
Auch die vierte Grundkonstruktion umfasst, wie schon die dritte, zwei Fälle
1. ) Der gegebene Winkel liegt der 2.) Der gegebene
größeren Seite gegenüber. Winkel liegt der kleineren Seite gegenüber.
Aufgabe (1. Fall):
Konstruiere ein Dreieck mit a = 3 cm, c = 5 cm und γ = 110°.
Konstruktionsplan:
Zunächst zeichnen wir die Seite a mit 3 cm und erhalten B und C. Anschließend tragen wir den Winkel γ ein. Nun stellen wir den Zirkel auf den Radius 5 cm und stechen ihn in Punkt B. Die Kreislinie schneidet die Seite b in einem Punkt. Hier liegt Punkt A. Zuletzt verbinden wir A und B miteinander.
Im zweiten Fall ergeben sich zwei Schnittpunkte durch die Kreislinie des Zirkels. Beide Schnittpunkte sind richtig und entsprechen der Aufgabenstellung des Dreiecks. Daher sollten sie auch beide eingezeichnet werden. Man erhält also zwei richtige Dreiecke.
Übungsaufgaben:
1. a = 5 cm; b = 3 cm; α = 50°
2. a = 3 cm; c = 5 cm; α = 30°
3. b = 6,5 cm; c = 4,2 cm; β = 140°
4. a = 4,8 cm; c = 4 cm; γ = 50°
5. a = 4,8 cm; b = 5 cm; β = 30°
6. b = 4 cm; c = 6 cm; β = 35°
7. b = 2,8 cm; c = 3,6 cm; γ = 80°
8. a = 6,2 cm; b = 7,5 cm; α = 45°
9. b = 5,5 cm; c = 3,8 cm; γ = 25°
Alle vier Grundkonstruktionen gemischt:
1.) a = 3,8 cm, β = 75°, γ = 38°
2.) b = 5,4 cm, α = 45°, γ = 50°
3.) c = 5,3 cm, β = 83°, γ = 57°
4.) a = 7,2 cm, b = 2,7 cm, c = 8 cm
5.) a = 4,5 cm, c = 3,5 cm, β = 63°
6.) a = 2,8 cm, c = 3,5 cm, α = 40°
7.) a = 3,2 cm, b = 4,4 cm, c = 4,1 cm;
8.) b = 3,9 cm, β = 40°, γ = 110°
9.) b = 2,6 cm, c = 4,2 cm, β = 25°
10.) b = 3,4 cm, c = 4,3 cm, α = 110°
11.) b = 5,4 cm, α = 45°, γ = 50°
12.) a = 4,3 cm, α = 72°, γ = 68°
13.) a = 5 cm, b = 7 cm, c = 8 cm
14.) b = 7,5cm, c = 4,7cm, β =111°
15.) a = 4 cm, c = 5 cm, γ = 58°
16.) c = 5,1 cm, β = 38°, γ = 62°
17.) a = 4,8 cm, b = 2,4 cm, c = 3,6 cm
18.) a = 5,2 cm, b = 3,8 cm, γ = 90°
19.) a = 5,8 cm, b = 4,5 cm, α = 65°
20.) a = 6,5 cm, b = 4,9 cm, β = 43°
21.) b = 5,2 cm, c = 3,5 cm, γ = 38°
22.) a = 8 cm, c = 5 cm, β = 25°
23.) b = 3,2 cm, α = 125°, γ = 25°
24.) c = 4,6 cm, α = 48°, β = 84°
25.) b = 2,8 cm, c = 6,4 cm, γ = 145°

