Freihandgeometrie 1
Ein Beitrag von Helga Keller
Das 5. Schuljahr bildet eine Schnittstellte zwischen dem Formenzeichnen der ersten vier Schuljahre und der Geometrie der folgenden Jahre. Im Mittelpunkt stehen die geometrischen Gesetzmäßigkeiten von Kreisen, Dreiecken und Vierecken, die aber nicht mit Geodreieck und Zirkel, sondern von Hand gezeichnet werden. Warum? Was den Kreis zum Kreis macht, erkennt man am besten, wenn man den Kreis durch die eigenen Gestaltungskräfte entstehen lässt. Und das ist gar nicht so einfach. Das Auge ist sehr kritisch, wenn es darum geht, ob der Kreis wirklich überall rund ist.
Kreis
In dieser Epoche bin ich von der ebenmäßigsten Form, die es gibt, ausgegangen: dem Kreis. Bei dieser Form, die wir in den vergangenen vier Jahren immer wieder gezeichnet hatten, gaben wir uns besonders viel Mühe. Wir begannen immer zuerst mit zartem Bleistiftstrich. Ein wenig Schwung war hilfreich: nicht zu schnell und nicht zu langsam. Es wurde korrigiert, auch radiert und die Verhältnisse ständig neu mit dem Auge vermessen. Das dauerte Zeit. Anschließend durften alle Formen farbig nach eigenen Vorstellungen gestaltet werden. Die folgenden Bilder sind SchülerInnenwerke.


Am jeweiligen Folgetag entdeckten wir gemeinsam im Unterrichtsgespräch die entsprechenden Gesetzmäßigkeiten. Auf der Rückseite skizzierten wir schlicht und nicht mehr farbig nochmals die Form und verschriftlichten ihre Eigenschaften.
Nachdem wir beim Kreis erkannt hatten, dass die Kreislinie vom Mittelpunkt überall gleichweit entfernt ist, konstruierten wir auf dem Schulhof mit Schnur und Kreide munter viele kleine und große Kreise. Wir probierten dies auch anschließend in kleinerem Maßstab zu zweit in unserem Heft. Das war nicht so einfach, wie man vielleicht denken mag.
Ellipse
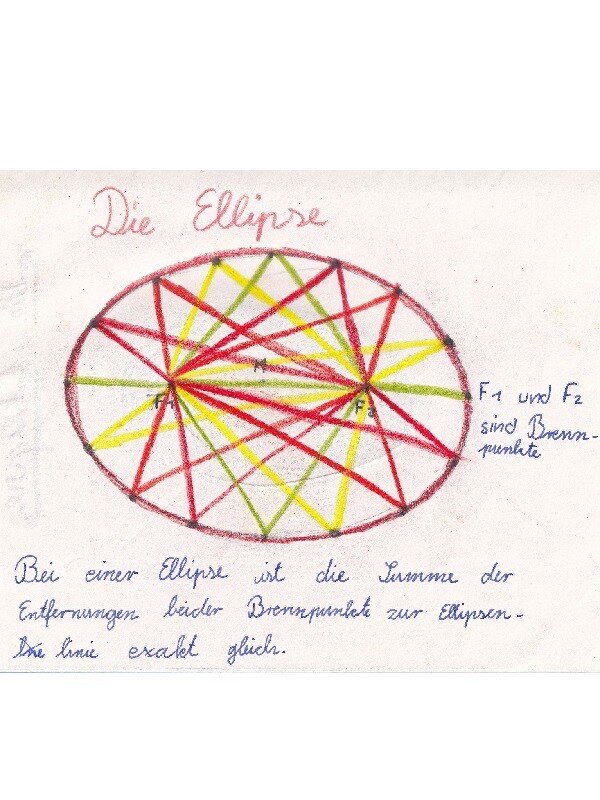
Die Ellipse hat nicht einen Mittelpunkt wie der Kreis, sondern zwei Brennpunkte. Zuerst haben wir die Ellipse ohne weitere Erklärung per Hand gezeichnet und am zweiten Tag auf dem Boden des Klassenraums mit Kreide und einem Faden konstruiert. Man beachte, dass der Faden nicht dehnbar sein sollte. Zu zweit haben die Schülerinnen und Schüler dies dann in ihrem Epochenheft versucht. Hierfür braucht man Geschick und Geduld. Die Gesetzmäßigkeit der Ellipse zu entdecken war die größte Herausforderung in dieser Epoche.

Strecke, Strahl, Gerade – der Winkel
Bevor wir zu den Vierecken und Dreiecken übergingen, klärten wir ein paar Begriffe.

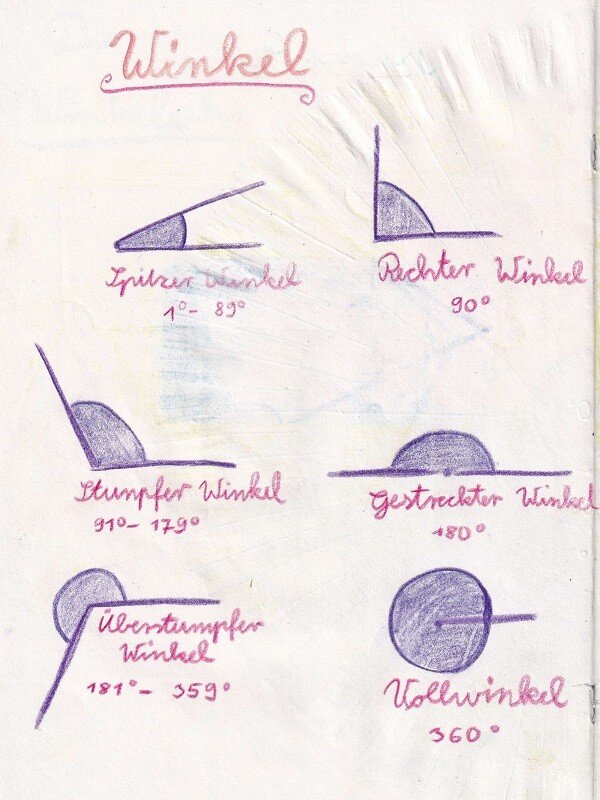
Die Winkeluhr fertigten wir doppelseitig an. Der innerste Kreis beschrieb 360°, der nächste Ring 180°, dann 90°, 30°, 10°, 5° und der äußerste Ring am Ende gab für ganz Geduldige 1° an. Nach Ferigstellung schlossen sich Übungen an, indem man nun mit zwei Stiften Winkelgrößen von 150°, 70°, 45° usw. zeigen konnte.

Vierecke
Die Vielfalt der Vierecke ist erstaunlich. Da gibt es das Quadrat, das Rechteck, das Parallelogramm, das gleichschenklige Trapez, das allgemeine Trapez, die Raute, den Drachen und das allgemeine Viereck.
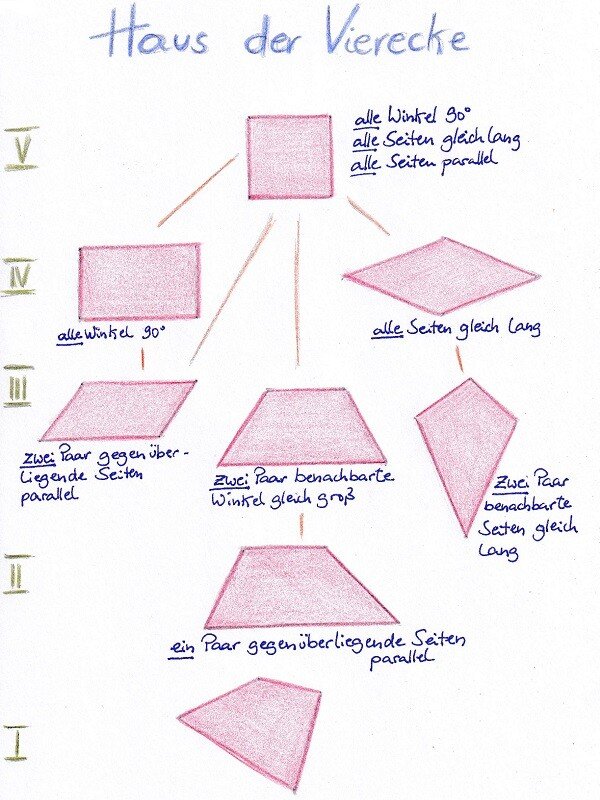
Sie lassen sich in das so genannte „Haus der Vierecke“ einordnen. Dies sollte erst im 6. Schuljahr geschehen. Für den Lehrer ist es allerdings wichtig zu wissen, welche Beziehung die Vierecke zueinander haben. In der nebenstehenden Skizze sind die einzelnen Stockwerke angegeben. Das Quadrat hat die meisten Eigenschaften. Es erfüllt aber auch die Eigenschaften aller anderen Vierecke. So ist ein Quadrat beispielsweise auch ein Rechteck oder ein Drache. Die unteren Stockwerke haben immer weniger Eigenschaften bis das allgemeine Viereck eigentlich gar keine eigenen mehr hat.
Um die Beziehung der Vierecke zu verdeutlichen, habe ich versucht, im Unterrichtsverlauf ein unteres Stockwerk immer aus einem höheren zu entwickeln. So wurde aus der Raute ein Drache oder aus dem Rechteck ein Parallelogramm. Es ergaben sich daraus einfache und schöne Formen.
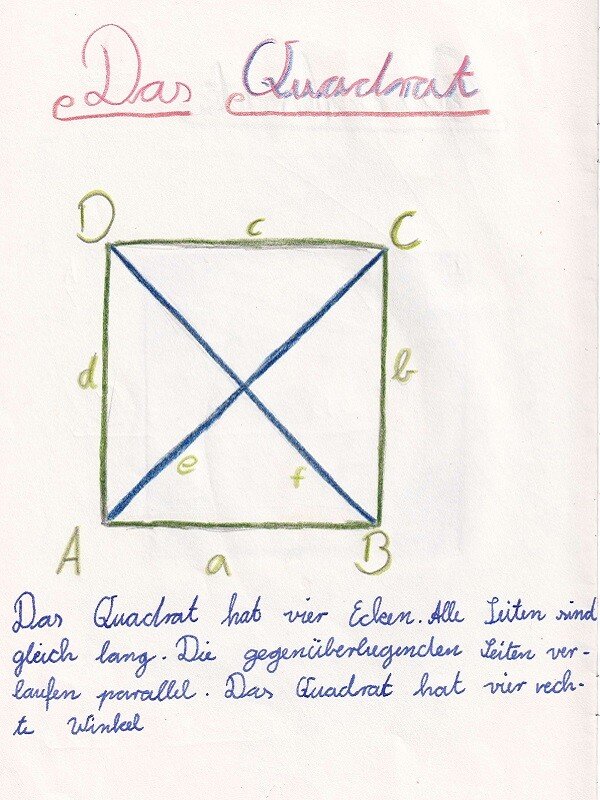
Das Quadrat:
- Symmetrieachsen: 4
- 4 Rechte Winkel
- 4 gleich lange Seiten
- gegenüberliegende Seiten sind parallel
- Diagonalen halbieren sich gegenseitig
- Diagonalen schneiden sich rechtwinklig
Das Rechteck:
- Symmetrieachsen: 2
- 4 Rechte Winkel
- gegenüberliegende Seiten sind gleich lang
- gegenüberliegende Seiten sind parallel
- Diagonalen halbieren sich gegenseitig
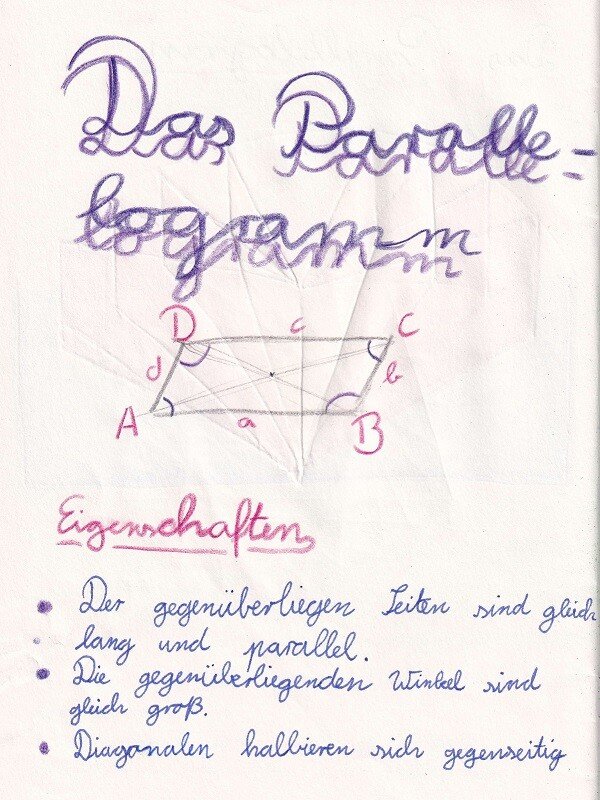
Das Parallelogramm
- gegenüberliegende Seiten sind parallel
- gegenüberliegende Winkel sind gleich groß.
- gegenüberliegende Seiten sind gleich lang
- Diagonalen halbieren sich gegenseitig
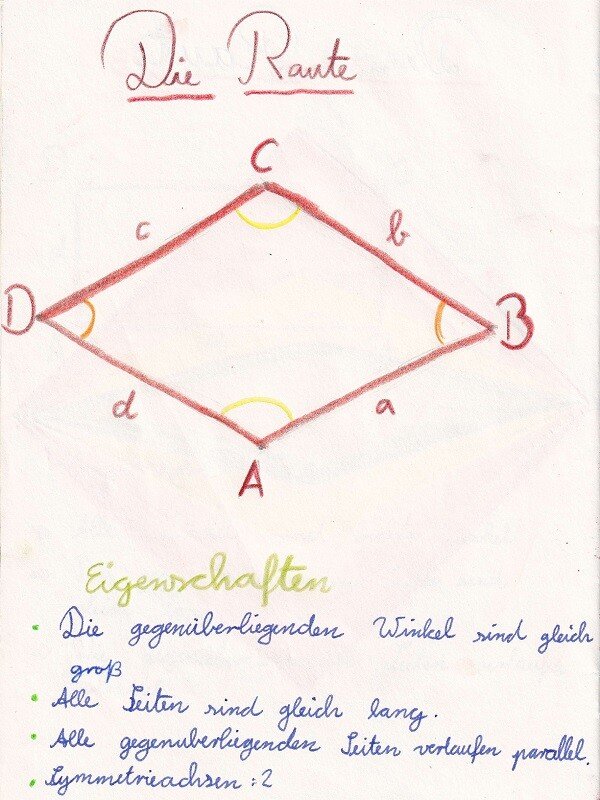
Die Raute:
- Symmetrieachsen: 2
- gegenüberliegende Winkel sind gleich groß.
- 4 gleich lange Seiten
- gegenüberliegende Seiten sind parallel
- Diagonalen halbieren sich gegenseitig
- Diagonalen schneiden sich rechtwinklig
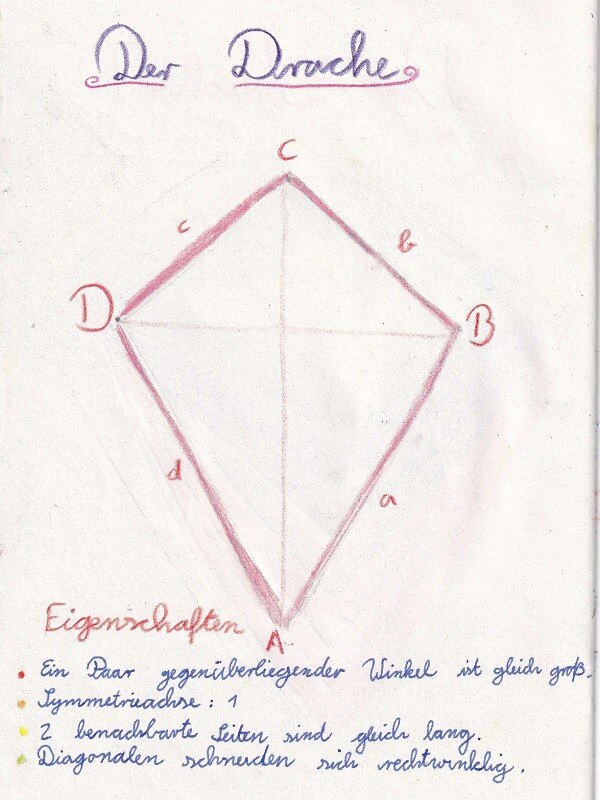
Der Drache:
- Symmetrieachsen: 1
- ein Paar gegenüberliegende Winkel sind gleich groß.
- je 2 benachbarte Seiten sind gleich lang
- Diagonale schneiden sich rechtwinklig
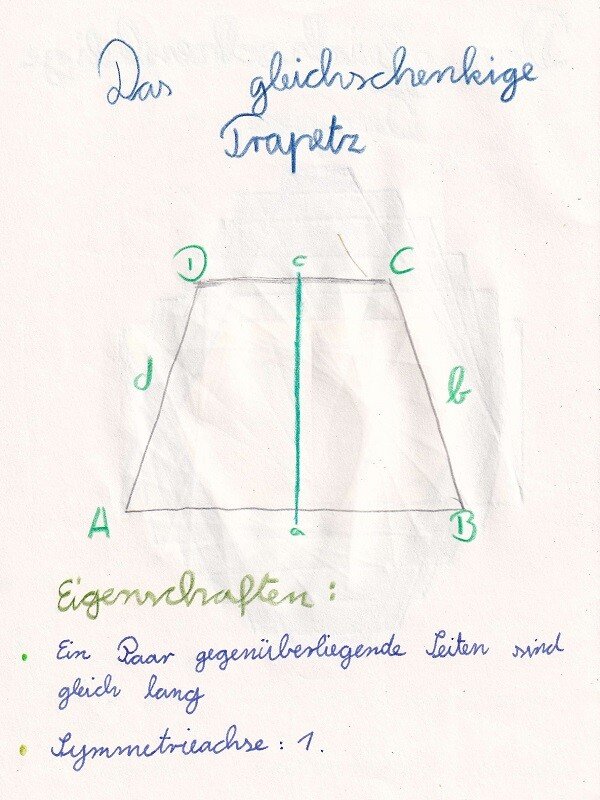
Das gleichschenklige Trapez
- Symmetrieachsen: 1
- je 2 benachbarte Winkel sind gleich groß.
- ein Paar gegenüberliegende Seiten sind parallel
- ein Paar benachbarte Seiten (Schenkel) sind gleich lang
- Diagonalen sind gleich lang
Das Trapez
- ein Paar gegenüberliegende Seiten sind parallel
Das allgemeine Viereck
- Es kann keine der oben aufgeführten Eigenschaften haben
- Für alle Vierecke gilt: Verbindet man die Seitenmitten ergibt dies ein Parallelogramm.






Dreiecke
Nun gingen wir zu den Dreiecken über. Hier gibt es im Grund nur drei verschiedene Arten: das gleichseitige, das gleichschenklige und das allgemeine Dreieck. Auch hier versuchten wir eines aus dem anderen zu entwickeln. Am Ende fehlte uns ein wenig die Zeit, weshalb die Rückseiten und das allgemeine Dreieck ausblieben.



