Die Platonischen Körper in der achten Klasse
Oder: Wie ordnen wir die Platonischen Körper?
Ein Beitrag von Walter Kraul
Jeder Waldorfschüler sollte im Rahmen der Geometrie auch den Platonischen Körpern begegnen dürfen.
„Sie gehören zu den schönsten und mathematisch betrachtet zu den reichhaltigsten Raumgebilden. Ihnen liegt eine Fülle harmonischer Eigenschaften zugrunde, wie sie bei keinen anderen geometrischen Körpern zusammen vorkommen.“ (Renatus Ziegler)
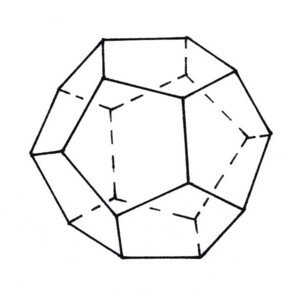
Diese fünf räumlichen Urformen gehören zum allgemeinen Kulturgut. Man kann sie mit den Schülern bauen. Dabei werden geometrische Konstruktionen praktisch angewendet und Genauigkeit geübt. Außerdem ist das eine großartige Schulung für das räumliche Vorstellungsvermögen. In diesen Körpern sind erstaunliche Verwandtschaften verborgen, es lohnt sich diese anzusehen.
Es gibt 120 verschiedene Möglichkeiten bei der Reihenfolge der Ineinanderschachtelung der Platonischen Körper. Nach meiner Ansicht ist eine davon aus weiter unten erläuterten Gründen die reizvollste: Im Dodekaeder steckt der Würfel - im Würfel steckt das Tetraeder - im Tetraeder steckt das Oktaeder - im Oktaeder steckt das Ikosaeder. Diese Ineinanderschachtelung mit einer achten Klasse herzustellen hat sich bewährt. Es folgt die Anleitung dazu.
MATERIAL:
- Als Material empfiehlt sich „Fotokarton“( 300 g/m2). Er ist in jedem Schreibwarengeschäft zu haben und es gibt ihn in vielen verschiedenen Farben, auf helleren sieht man die Bleistiftstriche besser.
- Für die Konstruktionen sind ein spitzer Bleistift (HB), ein Zirkel und ein Geodreieck (Basis 23 cm) geeignet.
- Zum Ausschneiden benötigen wir eine Schere und zum Anritzen der Kanten, die umgebogen werden, ein spitzes Messer (zur Not geht auch die Schere).
- Als Klebstoff eignet sich UHU-Alleskleber (nicht lösungsmittelfrei und nicht UHU-Kraft).
- Aus einem Fotokarton (50 cm x 70 cm) kann man in der im Folgenden empfohlenen Größe 2 ½ Dodekaeder, 4 Würfel, 8 Tetraeder, 14 Oktaeder und 20 Ikosaeder bei geschickter Einteilung bekommen.
WÜRFEL
Wir beginnen mit dem Bau des bekanntesten Vertreters der Platonischen Körper, mit dem Würfel. Die Kantenlänge 8 cm hat sich bewährt. Wir zeichnen so genau wie möglich die sechs Quadrate zusammenhängend in einem „Netz“.
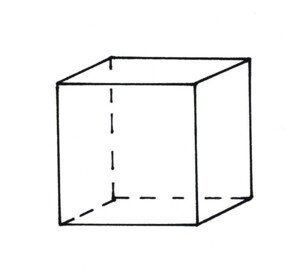
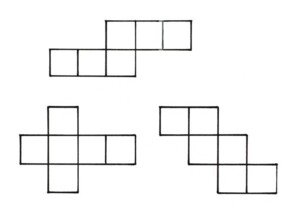
Es gibt elf verschiedene Netze, die drei wichtigsten sind in dem Bild rechts dargestellt. Wir denken auch daran, die zum Zusammenkleben nötigen Laschen (etwa 1cm breit) anzubringen. Eine Seite wird der aufklappbare Deckel sein, er bekommt auch Laschen. Letztere werden später nach innen geknickt, aber nicht verklebt.
TETRAEDER
Es folgt das Tetraeder. Die theoretisch richtige Kantenlänge ist die Würfeldiagonale mit 8 V2 cm = 11,3 cm Länge. Wir müssen jedoch die Stärke des Kartons berücksichtigen und runden auf 11 cm ab.
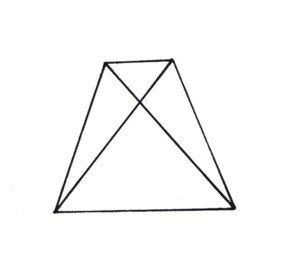
Der Bau ist einfach. Das Netz besteht aus vier aneinander liegenden gleichseitigen Dreiecken. An den Deckel denken! Das Tetraeder wird mit einer Kante voraus in den Würfel gesteckt.
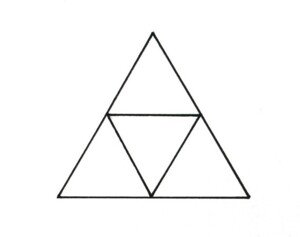
OKTAEDER
Nun das Oktaeder. Die Kante ist halb so lang wie die des Tetraeders, aber wir müssen wieder die Kartonstärke berücksichtigen und nehmen daher als Kantenlänge 5,4 cm.
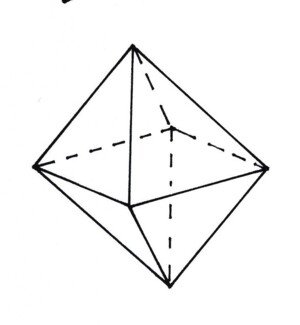
Diesen Körper setzen wir am besten aus zwei gleichen Teilen zusammen, aus zwei vierseitigen Pyramiden. Die nötigen gleichseitigen Dreiecke entnehmen wir einem Kreis. Der aufklappbare Deckel muss diesmal aus zwei Dreiecken bestehen, die zusammenhängen können, aber nicht müssen. Das Oktaeder berührt beim Einlegen mit jeder zweiten Seite eine Tetraederseite von innen. Das Mittelstück unserer Reihe ist damit fertig.
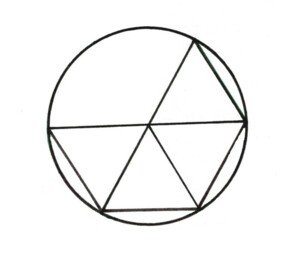
IKOSAEDER
Nun folgt als Kern der innerste Körper, das Ikosaeder. Diesmal ist es komplizierter, die richtige Kantenlänge zu finden. Acht von den 20 Ikosaederflächen liegen in den Oktaederflächen, aber verdreht. Die Ikosaederecken teilen die Oktaederkanten im goldenen Schnitt.
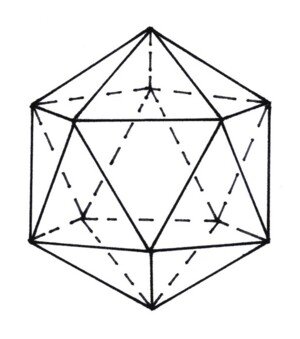
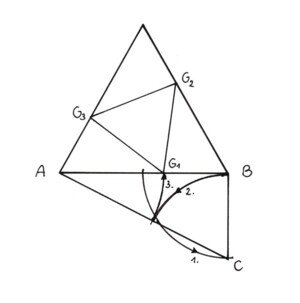
Die Konstruktion des goldenen Schnittes ist in dem rechten Bild dargestellt: Wir zeichnen eine Oktaederkante AB (5,4 cm). Diese Strecke halbieren wir im Punkt M. Sodann errichten wir in B das Lot nach unten und machen es so lang wie MB (Zirkel!), der neue Punkt heißt C. Die Verbindung AC vervollständigt das „Dreieck des Eudoxus“. Von C aus tragen wir BC auf die neue Verbindung AC ab und erhalten so den Punkt D. Abschließend tragen wir von A aus AD auf AB ab und erhalten so den goldenen Teilpunkt G1. Wir ergänzen die Zeichnung durch errichten eines gleichseitigen Dreiecks auf der Basis AB nach oben und tragen dort die weiteren zwei Teilpunkte G2 undG3 ein. Die Verbindung letzterer gibt uns ein Ikosaeder-Dreieck. Durch Abmessung kommen wir zu 2,9 cm, wieder kürzen wir wegen der Kartonstärke um 2 mm und erhalten 2,7 cm.
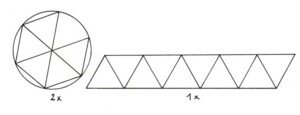
Das Ikosaeder bauen wir uns mit der erhaltenen Kantenlänge aus drei Teilen zusammen. Der erste Teil besteht aus zehn Dreiecken in einer Reihe. Wir geben ihnen Laschen und kleben sie zu einem Ring zusammen. Der zweite und dritte Teil sind zwei gleiche fünfseitige Pyramiden. Wir bekommen sie aus einem Kreis mit dem Radius der Kantenlänge 2,7 cm. Diese beiden „Hüte“ kleben wir auf die Laschen des Gürtels. Das Ikosaeder braucht als innerster Kern keinen Deckel. – Jetzt können wir bereits vier Körper ineinander stecken.
DODEKAEDER
Es fehlt nur noch die Umhüllung des Würfels durch den letzten und schönsten Körper, den Dodekaeder. Wieder müssen wir die richtige Kantenlänge herausbekommen. Die Würfelkante ist eine Diagonale der Dodekaeder-Fünfecks-Fläche. Jede Dodekaeder-Fläche hat fünf solche Diagonalen, die das bekannte Pentagramm bilden. Wir haben also zu der anfangs verwendeten Würfelkante von 8 cm Länge ein passendes Fünfeck zu konstruieren. Wieder spielt der goldene Schnitt eine wichtige Rolle.

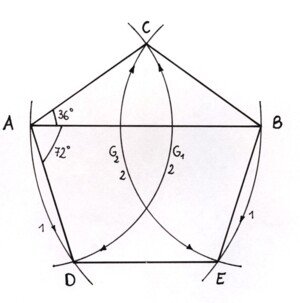
Durch die vom Ikosaeder schon bekannte Konstruktion teilen wir die Würfelkante AB (8 cm) im goldenen Schnitt und erhalten G1 und spiegelbildlich dazu G2 .Mit der Strecke AB im Zirkel schlagen wir um deren Endpunkte Kreisbögen nach unten. Anschließend nehmen wir die Spanne AG1 (größere goldene Teilstrecke) in den Zirkel und schlagen Kreisbögen um A und um B. Die Schnittpunkte der Kreisbögen geben uns die drei fehlenden Fünfeckspunkte C, D und E. Diese Konstruktion ist heikel, daher empfiehlt es sich, die neu entstandenen Winkel zu prüfen, sie müssen 36° bzw. 72° haben. Man kann auch mit diesen Winkeln und dem Winkelmesser von Anfang an arbeiten. Die gesuchte Kantenlänge des Dodekaeder-Fünfecks kann jetzt abgemessen werden, es ergeben sich 4,9 cm, die wir diesmal auf 5,1 cm wegen der Papierdicke vergrößern.
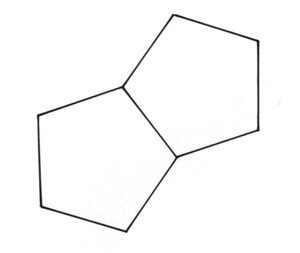
Am besten setzen wir diesen Mantelkörper aus sechs Fünfecks-Zwillingen zusammen. Dazu konstruieren wir uns durch Spiegelung an einer Fünfeck-Seite eine Schablone auf einen separaten Karton und schneiden sie großzügig aus. Mit der Zirkelspitze stechen wir auf den richtigen Karton die acht Punkte durch, geben jeder zweiten Seite eine Lasche, ritzen und schneiden aus, sechs Mal. Vier dieser Teile lassen sich problemlos zusammenkleben.
Aus den letzten beiden machen wir ein „Walmdach“ als Deckel, dazu muss das letzte Fünfeckspaar getrennt werden, eine Diagonale wird zum Scharnier (einritzen!) und in einer weiteren Diagonale wird geschnitten. Jetzt kann man den Würfel mit den drei aus Dreiecken bestehenden anderen Platonischen Körpern darin im Dodekaeder versenken und den Deckel schließen. Der Würfel berührt das umschließende Dodekaeder nur mit seinen acht Ecken. Damit ist die praktische Tätigkeit beendet.
NÄHERE BETRACHTUNG DER PLATONISCHEN KÖRPER
Als Zusammenfassung erstellen wir eine Tabelle in der sonst üblichen Reihenfolge, geordnet nach steigender Flächenzahl.
Name Flächen Ecken Kanten
Tetraeder 4 dreieckige 4 dreiflächige 6
Würfel 6 viereckige 8 dreiflächige 12
Oktaeder 8 dreieckige 6 vierflächige 12
Dodekaeder 12 fünfeckige 20 dreiflächige 30
Ikosaeder 20 dreieckige 12 fünfflächige 3
So wie wir bei den Flächen „dreieckig“, „viereckig“ oder „fünfeckig unterscheiden, können wir entsprechend auch die Ecken „dreiflächig“, „vierflächig“ oder „fünfflächig“ nennen. Mit gleichem Recht könnte auch nach der steigenden Anzahl der Ecken geordnet werden. Sollen wir beim Ordnen den Flächen oder den Ecken den Vorzug geben?
POLARITÄTEN: ECKEN - FLÄCHEN
Wir stellen fest, dass es offensichtlich zwei zusammengehörige Paare gibt, nämlich einerseits den Würfel und das Oktaeder und andererseits das Dodekaeder und das Ikosaeder. Der eine Teil dieser beiden Paare hat so viele Flächen wie der andere Ecken hat und so viele Ecken wie der andere Flächen hat. Nicht nur die Anzahl bleibt erhalten, auch die zugehörige Zähligkeit bleibt erhalten beim Übergang von der Ecke des einen Körpers zur Fläche des anderen und umgekehrt. So hat der Würfel z.B. sechs viereckige Fächen und das Oktaeder sechs vierflächige Ecken. Andererseits hat der Würfel acht dreiflächige Ecken und das Oktaeder acht dreiseitige Flächen. Beide Körper haben gleich viele Kanten. Man nennt zwei Körper mit diesen Beziehungen „polar“ zueinander. Das Tetraeder hat so viele Ecken wie es Flächen hat, beide dreizählig, daher sagt man, es sei zu sich selbst polar.
Unter „polarisieren“ verstehen wir, einen Tausch vorzunehmen: Anstatt Flächen setzen wir Ecken, statt Ecken Flächen, dabei verändern wir die Zahlen nicht. Aus einer dreieckigen Fläche z.B. wird eine dreiflächige Ecke. Die Anzahl der Kanten bleibt unverändert. So kommen wir von einem Würfel zum Oktaeder, vom Dodekaeder zum Ikosaeder und umgekehrt. Wie wir gleich sehen werden, wird beim Polarisieren auch außen zu innen und umgekehrt.
Die hier zum Bau vorgeschlagene Reihenfolge (1. Bild) ist eine andere als die in der Tabelle. Es lassen sich folgende Auffälligkeiten in unserer Reihenfolge feststellen, die alle an Hand der Modelle leicht nachzuvollziehen sind:
- Das äußere Dodekaeder ist polar zum innersten Körper, dem Ikosaeder. Der Würfel als zweiter Körper von außen ist polar zum Oktaeder, dem zweiten von innen. In der Mitte der Reihe befindet sich das zu sich selbst polare Tetraeder. Es herrscht also eine schöne, symmetrische Ordnung, die in Abb.1 in einer Reihe verwendet wurde.
- Der äußerste Körper ist von fünfeckigen Flächen gebildet, der nächste nach innen von viereckigen, dann folgt ein aus dreieckigen Flächen aufgebauter Körper.
Die Anzahlen der Flächen sind: 12, 6, 4.
Polarisiert: Der innerste Körper ist von fünfflächigen Ecken gebildet, der nächste nach außen von vierflächigen, dann folgt ein aus dreiflächigen Ecken aufgebauten Körper.
Die Anzahlen der Ecken sind: 12, 6, 4.
- Entsprechend stellen wir fest:
Der äußerste Körper hat dreiflächige Ecken, der nächste auch und ebenso der mittlere.
Die Anzahl der Ecken: 20, 8, 4.
Polarisiert: Der innerste Körper hat dreieckige Flächen, der nächste auch und ebenso der mittlere.
Die Anzahl der Flächen: 20, 8, 4.
Die dreiflächigen Ecken sind also außen und die dreieckigen Flächen innen. Das Tetraeder in der Mitte hat beides. In der Reihe von Abb.1 stehen links die drei Körper mit dreiflächigen Ecken und rechts die drei Körper mit dreieckigen Flächen, sich in der Mitte im Tetraeder überschneidend.
- Es liegen die vier Tetraeder-Ecken in vier von den acht Würfel-Ecken.
Polarisiert kommen wir zur Aussage: Es liegen vier Tetraeder-Flächen auf vier von den acht Oktaeder-Flächen. Auch dieser Satz ist richtig, er lässt sich leicht nachprüfen.
- Die acht Würfel-Ecken liegen in acht von den zwanzig Dodekaeder-Ecken.
Polarisiert: Die acht Oktaeder-Flächen liegen auf acht von den zwanzig Ikosaeder-Flächen. Wieder ein polarer und richtiger Satz.
- Die sechs Ecken des Oktaeders liegen in den sechs Kanten-Mittelpunkten des umhüllenden Tetraeders. Andererseits kann man polar sagen: Die sechs Flächen des Würfels sind die sechs Kanten-Mittelflächen des eingeschlossenen Tetraeders. Wir erkennen, wie zum Kanten-Mittelpunkt eine Kanten- Mittelebene polar ist, in unserem Fall realisiert durch eine Tetraeder-Kante und ein Würfel-Ebene. Umhüllend und eingeschlossen sind offenbar auch zwei polare Begriffe.
- Wenn wir die ganze hier verwendete Reihe polarisieren, bekommen wir die gleiche Reihe wieder. Aus dem Dodekaeder mit dem Würfel darin wird ein Ikosaeder mit einem Oktaeder herum, aus der äußeren Situation wird also die innere. Aus dem Würfel mit dem Tetraeder innen wird polar das Oktaeder mit dem Tetraeder herum. Die ganze Reihe ist zu sich selbst polar. Natürlich ist diese Reihenfolge auch beim Aufreihen nebeneinander, wie in Abb.1, berechtigt.
PROJEKTIVE GEOMETRIE
Diese leicht nachzuvollziehenden Verhältnisse führen ein in den bei der Projektiven Geometrie so bedeutsame Vorgang des Polarisierens. Ein Teil der eingangs erwähnten „harmonischen Eigenschaften“ ist nun aufgezeigt. Einer achten Klasse kann man, so meine ich, dieses „offenbare Geheimnis“, das die Platonischen Körper in sich bergen, anvertrauen.
FERTIG, ABER WOHIN DAMIT?
Ein Problem besonderer Art entsteht, wenn die Platonischen Körper fertig gebaut sind: Wohin damit? Man kann ein Mobile daraus machen und dieses aufhängen. Man kann aber auch die Eigenart der Platonischen Körper ausnützen, dass sie sich ineinander fügen lassen. Tatsächlich passen in jeden Platonischen Körper die vier anderen in einer bestimmten Weise hinein. Folglich kann man die Modelle Raum sparend ineinander verschachteln, ähnlich wie die „russischen Puppen“. Beim Auspacken staunt jeder Zuschauer.
Zur Lage der einzelnen Platonischen Körper sei bemerkt: Johannes Kepler hat in seinem Büchlein „Vom sechseckigen Schnee“ (Geschenk an einen Freund) den Würfel als „männlich“ charakterisiert und das Oktaeder als „weiblich“. Diesen Bezeichnungen kann man sich nach meiner Ansicht anschließen und dem männlichen Würfel einen festen Stand auf einer Fläche geben. Zum weiblichen Oktaeder passt hingegen mehr die neckische Lage auf der Ecke. Man kann das zum Würfel verwandte Dodekaeder wieder auf eine Fläche stellen und das dem Oktaeder nahe Ikosaeder auf eine Ecke. Das Tetraeder ist noch unentschieden und steht gerne auf einer Kante. Bei den einrahmenden Nachbarn, im auf einer Fläche stehenden Würfel und um auf einer Ecke stehenden Oktaeder steht das Tetraeder auf einer Kante.
Zum Stehen auf einer Ecke verwendet man ringförmige Unterstützungen oder man hängt Oktaeder oder Ikosaeder an einer Ecke auf. Beim Tetraeder hätte das Stehen auf einer Fläche oder das Hängen an einer Ecke die gleiche Wirkung. Es bekommt eine keilförmige Unterstützung oder wird an einer Kantenmitte aufgehängt.

