Labyrinthe müssen nicht verwirren
Ein Beitrag von Thomas Peek
Geometrische Konstruktionen werden normalerweise um den zentralen Blattmittelpunkt M, seltener in einem vorgegebenen Raster ausgeführt. Ab etwa der achten Klasse werden daneben auch Konstruktionen um exzentrische Punkte geübt. Nicht nur an heilpädagogischen Schulen können solche Zeichnungen Schüler und Lehrer fordern. Als zum Schuljahresende mehrere dieser Konstruktionszeichnungen zwar vorbereitet, aber schließlich doch nicht ausgeführt blieben, entstand die Idee für diesen Aufsatz. Gewählt wurde ein heilpädagogisches Thema, das Labyrinth.
Warum Zirkelgeometrie?
Ab der 6. Klasse zeichnen viele Schüler gerne und allmählich ausdauernder geometrische Muster mit Zirkel und Lineal[1]. Das wird im Unterricht angeleitet und von den Teenagern abwechslungsreich geübt. Bald zieren die Pinnwand im Klassenraum, natürlich auch manche Heftseite immer anspruchsvollere Konstruktionen. Einzelne Schüler trennen sich zuweilen sogar während der Pausen nur ungern von ihrer Konstruktion[2]. Merklich wächst durch diese Art des Zeichnens sowohl das Raumvorstellungsvermögen, als auch die individuelle Konzentration und Verlässlichkeit.
Eine exakte Konstruktion erfordert zunächst innere Vorbereitung, während der die Schüler zur Ruhe finden. Bleistift, Zirkel und Lineal müssen gespitzt, einsatzbereit und vollständig vorliegen, bevor der Blattmittelpunkt zunehmend treffender festgelegt wird. Jede nun beginnende Konstruktion birgt für Lehrer und Schüler den unschätzbaren Vorteil, dass bereits auf den ersten Blick sich Stärken und Schwächen der geometrischen Umsetzung zeigen. Wurde mit stumpfem Stift gezeichnet, ein falscher Abstand gewählt oder konzentrationslos Arbeitsschritte übersprungen, fällt dies sofort auf und braucht nicht diskutiert werden. Eine Konstruktion wird entweder exakt und wie vorgegeben ausgeführt, oder nicht!
Warum das Motiv des Labyrinths?
Die ursprüngliche Bedeutung des archaischen Wortes "Labyrinth" ist unsicher. Es wäre verführerisch, jedoch zu einfach, würde man den Begriff vom lateinischen "labor intus" etwa: "Arbeit am Inneren" ableiten. Waldorfschülern fällt oft das Labyrinth des Daedalos auf Kreta ein. Hier lebte das Mischwesen Minotaurus gefangen. Aus diesem Labyrinth konnte niemand entkommen, auch nicht die Menschenopfer, welche der Minotaurus verschlang. Schließlich löste Theseus dieses blutige und psychologische Drama mit Hilfe des Ariadnefadens und seines Schwertes.
Natürlich fallen vielen Schülern gerade jetzt im Herbst auch die fälschlicherweise als Labyrinth bezeichneten Irrgärten in Maisfeldern oder hinter hohen Hecken ein. Das sind Gänge, in denen man sich verläuft, sich sogar verirren soll. Im Gegensatz zum Labyrinth ist ein Ausweg aus dem Irrgarten nur durch Zufall oder mit Hilfestellungen zu finden. Man verliert dort jeden Überblick. Im Irrgarten kann bald ein Gefühl der Ausweglosigkeit entstehen. Dann wird man atemlos. Der Besuch eines Irrgartens wird schnell zur michaelischen Herausforderung, wie Schüler oft zu berichteten wussten.
Anders als im Irrgarten soll man im Labyrinth seine Mitte (wieder) entdecken. Ein gewundener Weg führt ohne Sackgasse oder Irrwege weiter bis zur Mitte. Hat man die Mitte nach vielen Wendungen erreicht, führt der verschlungene Pfad genauso sicher wieder hinaus. Markierungen sind normalerweise ebenerdig oder flach ausgeführt, so behält man im Labyrinth den Überblick. Im klassischen Labyrinth wird hoffentlich im übertragenen Sinn der eigene Weg gefunden, dem man folgt.
Wie wird ein klassisches kretisches Labyrinth, das sog. "Ariadnelabyrinth" konstruiert?
Klassische Labyrinthe wirken, anders als deren meiste mittelalterliche oder neuzeitliche Nachfolger, zwar wie um einen zentralen Mittelpunkt konstruiert, sie sind es jedoch nur ausnahmsweise. Regelmäßig besitzen sie 7 Umgänge. Ein Konstruktionsweg des Ariadnefadens für DIN A3 Blätter wird hier vorgeschlagen. Vielleicht findet jemand einen einfacheren.
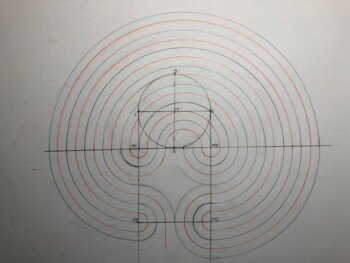
Konstruktionsbeschreibung
- Zeichne im Querformat. Der Zeichnungsmittelpunkt M liegt 13 cm unterhalb der Mitte des oberen Blattrandes (21 cm von den Seitenrändern).
- Ziehe um M einen Kreis r=4cm.
2.1) Zeichne in diesen Kreis die Mittelwaagerechte und konstruiere die Mittelsenkrechte.
2.2) Die Schnittpunkte am Kreis heißen (an der Mittelwaagerechten links beginnend) A, B, C, D.
2.3) Nimm A---M in den Zirkel (=4cm).
2.4) Ziehe Teilkreise um A und um B, die einander schneiden. Der Schnittpunkt heißt M1.
2.5) Ziehe Teilkreise um B und um C, die einander schneiden. Der Schnittpunkt heißt M4.
2.6) Verbinde M1 über B mit M4. Verlängere die Strecke zu beiden Seiten.
2.7) Verbinde A mit M1 und verlängere die Strecke um mindestens 10cm.
2.8) Verbinde C mit M4 und verlängere die Strecke um mindestens 12cm.
2.9) Nimm M1---M4 (=8cm) in den Zirkel.
2.10) Trage mit dem Zirkel von M1 und von M4 an den verlängerten Geraden jeweils die eingestellte Strecke M1---M4 ab.
2.11) Die neuen Schnittpunkte heißen M2 und M3. Verbinde M2 mit M3. M1, M2, M3, M4 bezeichnen ein Quadrat mit der Seitenlänge von 8cm, genau 2 cm unterhalb von M.
2.12) Markiere an den Quadratseiten Zentimeterabstände. - Verlängere die Strecken M1 --- M4 über beide Punkte um mindestens 12cm.
- Ziehe um M1 und um M4 Halbkreise nach unten mit r= 1cm und r=3cm; um M2 solche Halbkreise nach rechts (r=3cm endet an der unteren Quadratseite), um M3 solche Halbkreise nach links. Anfangs- und Endpunkt der Halbkreise sind jeweils die verlängerten Geraden.
- Markiere an der Strecke M1 - M4 den Punkt bei 5cm (1cm rechts von B). Er heißt E.
Ziehe steigende Halbkreise um E mit r= 2cm, r= 4cm, r= 6cm, r= 8cm, r= 10cm, r= 12cm, r= 14cm. Anfangs- und Endpunkt der Halbkreise sind jeweils die beidseitig verlängerte Gerade M1 --- M4. - Ziehe um M1 Viertelkreise mit r= 5cm, r=7cm, r=9cm. Die Anfangspunkte der Viertelkreise liegen auf der verlängerte Gerade M1 --- M4. Die Endpunkte liegen auf der verlängerte Gerade M1 --- M2.
- Ergänze um M4 die fehlenden Viertelkreise r= 5cm, r=7cm, r=9cm, r=11cm.
Gezirkelt wurde der Ariadnefaden. Ziehe ihn rot nach. Durch eigene Überlegungen kannst du nun leicht die Labyrinthgänge ergänzen und in der eigenen Zeichnung schwarz hervorheben.
Das Knidos - Labyrinth
Im Südwesten der Türkei liegt, etwa gegenüber der griechischen Insel Kos, die antike Stadt Knidos. Im dortigen korinthischen Tempel wurde ein Bruchstück aus schwarzem Marmor entdeckt, in das ein bekanntes spätantikes Labyrinth - Motiv geritzt ist. Es hat 7 Umgänge, ausgehend vom zentralen Kreuz. Die griechische Inschrift oberhalb des Labyrinths lautet: KYRIE BOETHIE, etwa "Herr, hilf!". Weitere Ritzungen, wie ein Kreuz mit den Buchstaben Alpha und Omega als Pendilien an den Armen, Palme und Kletterpflanze erlauben die Datierung allgemein in die Spätantike[3]. Inzwischen wurde in der Literatur für diesen Labyrinth - Typ der Begriff Knidos- Labyrinth üblich.
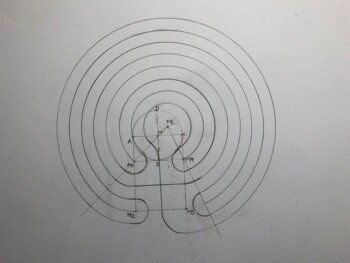
Konstruktionsbeschreibung
Die Konstruktionszeichnung auf DIN A3 Blättern wird hier vorgeschlagen. Zeichne im Querformat. Vielleicht findet jemand einen einfacheren Konstruktionsweg.
- Bestimme den Blattmittelpunkt M.
- Ziehe um M einen Kreis r=2cm.
2.1) Zeichne in diesen Kreis die Mittelwaagerechte und konstruiere die Mittelsenkrechte.
2.2) Die Schnittpunkte am Kreis heißen (an der Mittelwaagerechten links beginnend) A, B, C, D.
2.3) Nimm A --- M in den Zirkel (=2cm).
2.4) Ziehe Teilkreise um A und um B, die einander schneiden. Der Schnittpunkt heißt M1.
2.5) Ziehe Teilkreise um B und um C, die einander schneiden. Der Schnittpunkt heißt M4.
2.6) Verbinde M1 über B mit M4.
2.7) Verbinde A mit M1 und verlängere die Strecke um mindestens 4cm.
2.8) Verbinde C mit M4 und verlängere die Strecke um mindestens 4cm.
2.9) Nimm M1 --- M4 (=4cm) in den Zirkel.
2.10) Trage mit dem Zirkel von M1 und von M4 an den verlängerten Geraden jeweils die eingestellte Strecke M1---M4 (=4cm) ab.
2.11) Die neuen Schnittpunkte heißen M2 und M3. Verbinde M2 mit M3. M1, M2, M3, M4 bezeichnen ein Quadrat mit der Seitenlänge von 4cm, genau 2 cm unterhalb von M. Markiere an den Quadratseiten Zentimeterabstände. - Verbinde die gegenüberliegenden Seitenmitten des Quadrates zum zentralen Kreuz.
- Konstruiere nun durch Kreuzung von Zirkelschlägen die Mitte des Labyrinths (ML): M1 --- ML = 4cm, M4 --- ML = 3cm.
- Verbinde ML mit M1 und mit M4. Verlängere die Strecken über die Eckpunkte des Quadrates hinaus um mindestens 6cm.
5.1) Radiere den Kreis um M. - Ziehe um ML Teilkreise mit r= 2cm, r= 3cm, r= 4cm ... r= 9cm. Die Teilkreise enden jeweils an den verlängerten Geraden ML --- M1 und ML --- M4.
- Verlängere die 5 äußeren dieser Teilkreise bis zu den Quadratseiten durch kurze Zirkelschläge um M1 und den äußeren durch einen kurzen Zirkelschlag um M4.
- Vervollständige die Konstruktion durch Halbkreise r= 1cm um M1, M2 und um M4. Ein letzter solcher Zirkelpunkt liegt auf der Verlängerung der Geraden ML --- M4 am Ende des Kreises r=7cm.
- Ein Viertelkreis r= 2cm um M1 endet bei B; ein Viertelkreis r= 2cm um M3 endet in der Mitte von M2 --- M3.
Ideen zu diesen und weiteren Labyrinth - Konstruktionen entstanden auch beim Rasenmähen. Vielleicht fühlt sich ja ein Leser herausgefordert und mäht, mit starker Kette etwa um Eisenstäbe sein Labyrinth. Auf dessen Fotos und Erfahrungen bin ich besonders gespannt.
[1] Gerne werden später exakt zu konstruierende Motive bereits in den Fächern Formenzeichnen oder Freihandgeometrie vorbereitet. Vgl. etwa R. Kutzli, Entfaltung schöpferischer Kräfte durch lebendiges Formenzeichnen (Schaffhausen 1998) Achte Folge, 323 mit Abb. 2.
[2] R. Steiner, Stuttgart, 25.08.1919, GA 293: ...auf Wiederholung und bewusste Wiederholung beruht alle Willenskultur".
[3] S. Lunden, A new labyrinth at Knidos. Cardroia 33 (2003), 6-12.

